Bernoulli Numbers Calculator

Bernoulli Numbers Calculator

Bernoulli Numbers Calculator is used to calculate the Bernoulli numbers with the help of a larger number.

What is the Bernoulli Number?

Bernoulli numbers are a sequence of rational numbers with important mathematical properties. They are denoted as “B_n”. Bernoulli numbers are named after the Swiss mathematician Jacob Bernoulli who made exclusive contributions to the field of mathematics.

Where “n” is a non-negative integer denoting the order of the Bernoulli number.

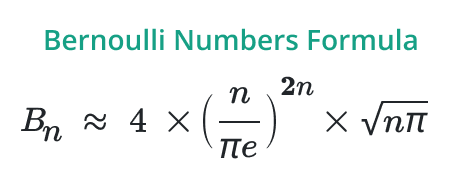
Bernoulli Numbers Formula

B_n = 4  (n / π e)²ⁿ ( √ n π)

n = order of Bernoulli number.

Methods to find Bernoulli’s numbers

There are several methods to calculate Bernoulli’s theorem but three main ones are discussed below. 

Akiyama-Tanigawa algorithm

This method involves constructing a triangular array of numbers, where the first row consists of the harmonic numbers, and the subsequent rows are obtained by taking the differences between consecutive elements in the previous row and multiplying them by (n+1). 

The first element of each row (excluding the first row) represents a Bernoulli number. 

Euler-Maclaurin Formula

This formula approximates integrals and sums in calculus and can be used to compute Bernoulli numbers when combined with the Riemann zeta function. The calculator above uses this method.

Explicit Sum Formula

It is finding Bernoulli numbers using the sum representation, which is not the most efficient method but is easier to understand. The nth Bernoulli number, B0, can be expressed as:

Bn = (-1)^n * n! * (Σ (1/k^(n+1))) for n > 0, where the summation runs from k = 1 to infinity.

For n = 0, B0 = 1.

In this formula, n! denotes the factorial of n, which is the product of all positive integers up to n (for example, 4! = 4 × 3 × 2 × 1 = 24).

How to calculate Bernoulli Number?

Example 1

If “n = 27” then calculate the Bernoulli number.

Solution

Step 1: Write the given large number

n = 27, B_n =?

Step 2: Write the formula of the Bernoulli number.

B_n = 4  (n / π e)²ⁿ ( √ n π)

Step 3: Put the values in the above formula.

B₂₇ = 4  (27 / π e)²ⁿ ( √27 π)

B₂₇ = 5.0307097e²⁶

B₂₇ = 5.0307097e²⁶ is the Bernoulli number of “n = 27”.

Example 2

if “n = 50” then calculate the Bernoulli number.

Solution

Step 1: Write the given large number

n = 50, B_n =?

Step 2: Write the formula of the Bernoulli number.

B_n = 4  (n / π e)²ⁿ ( √ n π)

Step 3: Put the values in the above formula.

B₅₀ = 4  (50 / π e)²ⁿ ( √50 π)

B₅₀ = 5.0307097e²⁶

B₅₀ = 5.0307097e²⁶ is the Bernoulli number of “n = 50”.

Applications of Bernoulli Numbers

Bernoulli numbers have a variety of applications in different branches of mathematics. Some of the key applications include:

Summation Formulas: Bernoulli numbers help to derive closed-form expressions for the sums of powers of consecutive integers, making it easier to compute these sums efficiently.

Euler-Maclaurin Formula: This formula is used to approximate integrals and sums in calculus. Bernoulli numbers play a crucial role in the coefficients of this formula.

Riemann Zeta Function: The analytic continuation of the Riemann zeta function, an essential tool in number theory and the study of prime numbers, rely on Bernoulli numbers.

Bernoulli Numbers Table:

Here's a table of the first few Bernoulli numbers:

This table shows the first few Bernoulli numbers, B_n, with their corresponding index (n) in the sequence. It highlights the pattern that all odd-indexed Bernoulli numbers greater than 1 equal zero.