To calculate result you have to disable your ad blocker first.
Ellipse Calculator
Put the values and hit on the calculate button to get the ellipse area, perimeter, and volume using this ellipse calculator.
Ellipse Calculator
Ellipse Calculator is an online tool that helps you perform various calculations related to ellipses such as area and perimeter
What is Ellipse?
An ellipse is a closed curve in a two-dimensional plane resembling an elongated circle. It is defined by two foci which are two fixed points inside the ellipse. From any point on the ellipse, the sum of the distances to the two foci equals the major axis and remains constant.
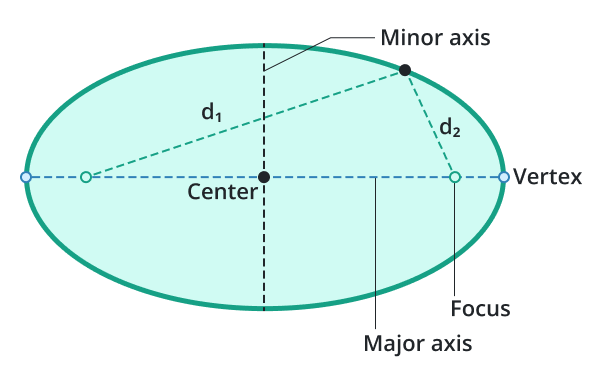
Formulas of Ellipse
Area of an Ellipse
The area A of an ellipse can be determined by using the formula given below:
A = π × r1 × r2
Where:
- A is the area of the ellipse
- r1 is the length of the axis
- r2 is the length of the other axis
Perimeter of an Ellipse
Finding the exact closed-form formula for the perimeter (P) of an ellipse is challenging, and it involves elliptic integrals. However, an approximate formula for the perimeter, known as Ramanujan's formula, provides a good estimation:
P ≈ [ 2 × π × Sqrt ((r1² + r2²)/2)]
Where:
- P is the perimeter of the ellipse
- r1 is the length of the axis.
- r2 is also the length of the other axis.
Volume of an Ellipse
The volume of an ellipse can be determined by following the steps given below:
Volume = [ (4/3) ×π×r1×r2×r3]
- r1 is the length of the axis
- r2 is the length of the axis
- r3 is the length of the axis
Ellipse Characteristics
The shape of an ellipse is defined by its eccentricity which measures how elongated the ellipse is.
- e = 0 represents a perfect circle (the two foci coincide at the center).
- 0 < e < 1 indicates an ellipse with varying degrees of elongation.
- e = 1 represents a degenerate ellipse, where the two foci are at the ends of the major axis, and the ellipse becomes a line segment.
How to find the area, perimeter, and volume of the ellipse?
Example
Calculate the area, perimeter, and volume of an ellipse when r1 = 21, r2 = 54, r3 = 18.
Solution
Area:
A = π × r1 × r2
A = 3.14 × 21 × 54
A = 3560.76
Perimeter:
P = [ 2 × π × Sqrt ((r1² + r2²)/2)]
P = [ 2 × 3.14 × Sqrt ((21² + 54²)/2)]
P = [ 2 × 3.14 × Sqrt ((3357)/2)]
P = 2 × 3.14 × Sqrt (1678.5)
P = 2 × 3.14 × 40.96
P = 257.2288
Volume:
V= [ (4/3) ×π×r1×r2×r3]
V = [ (4/3) ×3.14×21×54×18]
V = (4/3) × 64093.68
V = 256374.72 / 3
V = 85458.24

