To calculate result you have to disable your ad blocker first.
Even or Odd Function Calculator
To use the Even or odd function calculator, enter the function and click calculate.
Even or odd function calculator
The even or odd function calculator will classify the input function as even, odd, or neither. This tool is especially useful for complex functions that include trigonometry, logarithm e.t.c.
What are even and odd functions?
Even functions are the ones that satisfy the following equation:
F (x) = F(-x)
This means for all x of this function if you put a negative value, the answer will be the same as the original value. Something like when f(x2) and x = -1, the answer is 1.
Such functions follow a symmetry in their graphs like parabola and cosx functions.
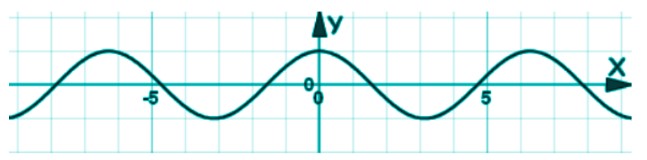
Cosine Function
Odd functions are the opposite of even. The equation that an odd function satisfies is:
F (x) = - F(x)
So, such functions solve to an opposite value of the original function. Exponents like x, x3, x5, e.t.c make an odd function. But it should be noted that not every even exponent is an even function and not every odd exponent is an odd function like (x + 1)4 and (x - 1)3.
Some functions are neither even nor odd. These are the functions that end up somewhere between the same and the exact opposite values.
How to identify even and odd functions?
Use the odd or even function calculator for this purpose. For identification without the use of the calculator, put the -x in the function.
Examples:
- Take the function -5x4 - 7. What does it look like? even or odd? It is always better to solve. Plug -x in the function.
= -5x4 - 7x2
= -5(-x)4 -7(-x)2
= -5(x)4 -7(x2)
We got the value we started with. This means the function above is even.
- The next function is 6x + 4x3. Is it even? You should never tell before solving it properly.
Put -x in the place of x.
= 6x + 4x3
= 6(-x) + 4(-x)3
= -6x -4x3
As you can see it will be plotted on the exact opposite side of the graph. Hence, it is an odd function.
- Lastly, we have the function 9x2 + x.
If you put -x in this function, it will solve to
= 9x2 + x
= 9(-x)2 + (-x)
= 9x2 - x
One half of this function is inverted while the other half remains the same. This means it is neither even nor odd.

