Acute Angle: Definition, Formula, and Calculations

A less-than-90-degree angle is expressly referred to as having an "acute angle" in this context. The word “acute” comes from the Latin word “acutus,” meaning “sharp” or “pointed,” which refers to the sharpness or narrowness of the angle.

In the Middle Ages, Islamic mathematicians made significant contributions to the study of angles, including the development of trigonometry, which is the study of the most famous Islamic mathematicians, al-Khwarizmi, wrote a treatise on the subject titled “The Book of Al-Jabr,” which included a table of sines for acute angles.

In this article, we will analyze the basic concept of an acute angle, elaborate on its formula and also discuss its application in daily life.

Introduction of Acute Angle

Acute angles are those that are less than 90 degrees. In other words, it is an angle that is "sharp" or "narrow," with its two rays or sides meeting at a point that is less than a right angle.

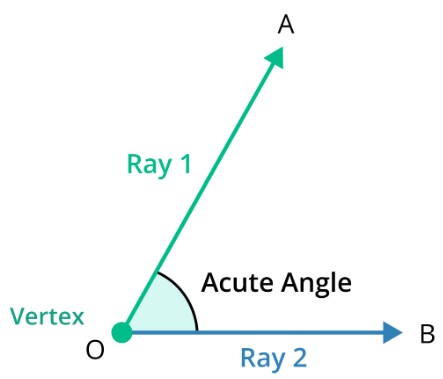
The term "acute" comes from the Latin word "acutus," meaning "sharp" or "pointed," which refers to the sharpness or narrowness of the angle. Acute angles are commonly found in geometric shapes such as triangles, where they form the smallest angle of the triangle.

Examples:

Angles 30^o, 45^o, 60^o are all examples of acute angles.

Acute Angle in mathematical form

In mathematical form, the acute angle can b represented in two ways:

• DMS or Sexagesimal system
• Radian or circular system

DMS or Sexagesimal system representation:

Way of representation in which angle expressed in Degree. minute and second.

For example, 13^o, 75^o 15’, 80^o.

Radian or circular system representation:

The method of angle representation of the form of pi “π” is known as the radian representation of angle.

Examples of an acute angle in the form of radian representation are π/3, π/12, 2π/7, etc.

Images of Acute Angle

The formula of Acute Angle

The following propositions are true for the side lengths of an acute triangle:

a² + b² > c²

b² + c² > a²

c² + a² > b²

where a, b, and c are the sides of the triangle.

Applications of Acute Angle

There are very interesting applications of an acute angle in various fields of daily life:

• An acute angle is used to form the letter "V".
• At some hours, the clock's hands form sharp angles. i.e., at 11:00.
• Inside the car, the speedometer and the dashboard's turn signal indication create steep angles.
• If we cut a pizza into four or more pieces, each piece will make an acute angle.
• The arrows for "On the way" and "NO Left Turn" both have an acute angle.

Different types of angles:

There are many types of angles in mathematical geometry but here we discuss only three major angles:

• Acute angle
• Right angle
• Obtuse angle

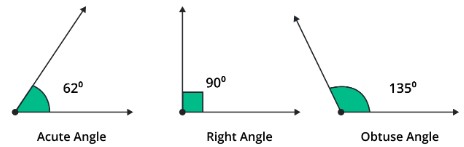
An acute angle is discussed in previous paragraphs now we discuss the other two angles

Right angle:

Right angles are angles that are exactly 90 degrees in length. In other terms, it is an angle created by two parallel lines that are 90 degrees apart from one another. A little square positioned at the angle's vertex serves as the sign for a right angle.

Due to their application in numerous computations and formulas, right angles are crucial in many subjects, including geometry, mathematics, and others.

An obtuse angle:

Obtuse angles are any angles that are greater than 90 degrees but less than 180 degrees. It is an angle that is "blunt" or "wide," with its two rays or sides coming together at a position that is larger than a straight angle.

The name "obtuse" derives from the Latin word "Obtusus," which means "dull" or "blunt," and refers to the larger angle that the two rays create. Obtuse angles, which make up the greatest angle of an obtuse triangle, are frequently encountered in geometric designs like triangles.

Acute Angle Examples

Example 1:

Find the acute angle which is one-fourth of the right angle.

Solution:

Right angle = 90

Acute angle = 1 / 4 of the right angle

Acute angle = 1 / 4 * 90

Acute angle = 90 / 4

Acute angle = 22.5^o                          

Example 2:

Find the complement of the acute angle of 20^o.

Solution:

The complement of an angle is minus it from 90^o.

Now, acute angle = 20^o

Complement angle = 90 – 20

Complement angle = 70⁰                               

Example 3:

Find the supplement angle of the acute angle of 80^o.

Solution:

The supplement of an angle is minus it from 180^o.

Now, acute angle =80^o

Supplement angle = 180 – 80

Supplement angle = 100^o          

Summary

In this article, we studied acute angles are those that are "sharp" or "narrow" in character and are fewer than 90 degrees in length.

Acute angles are used in different fields and make easy our life. Here we discussed the basic concept of an acute angle, its history of invention, and the representation of acute angles in different ways.