To calculate result you have to disable your ad blocker first.
Area of a Circle: Definition, Formulas, and Examples
Publish Date: 08 Aug, 2023
Table of Content
A circle is a unique geometrical shape that appears in uncountable forms, from nature’s graceful leaf to the wheels that make our journey easier. In the world of mathematics, the circular area concept is very important.
The concept of the circular area allows us to evaluate the space between the circle, providing detailed knowledge about the circle. Circle plays a very important role in geometrical shapes because it is known as the origin of the other shapes.
Definition of Area of Circle
The area of a circle is known as the range covered by a circle in a 2D plane. In basic terms, the area of a circle is the area covered by a circle inside its boundary or circumference.
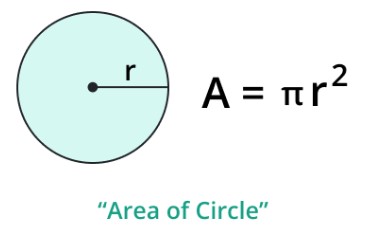
Here,
- A = Area of a circle is
- r = Radius of a circle
- π = Represents the pi which is constant.
Formulas for the Area of a circle
Formulas for the area of a circle are as follows:
- A = π*r2
- A = π*(d/2)2
- A = (π/4) *d2
- A = C2 / 2π
Sections of a circle
“A circle is a circular curve in which all the points have an equal distance from the center”. Clocks, wheels, pizzas, and other daily objects are examples of circles. Some sections of a circle are as follows.
- Radius of a circle
- Diameter of a circle
Basically, the circle is a composition of these two parts.
Radius
The radius of a circle mention to the distance covered from its edge to the center point. This critical attribute is represented by the symbol’s "r" or "R."
The following is the formula for the radius of the circle
"R = D / 2" or "r = d / 2"
Diameter
The line that divides a circle into two equal parts and passes through its center is represented graphically by the diameter of the circle. The letter "d" or the letter "D" stands in for it.
The diameter is sometimes referred to as the radius's double length. To determine the diameter, we employ the following formulas:
"D = 2R" or "d = 2r"
Applications
Some applications of the area of a circle are as follows:
Construction
Architects and civil engineers use the area of circles when designing structures such as circular buildings, arches, and circular ponds.
Physics
Calculating the areas of circular objects is crucial in various physical calculations, such as determining the cross-sectional area of cylindrical pipes or the surface area of rotating objects.
Automobile Industry
In automobile engineering, calculating the area of circular components like pistons, cylinders, and rotors is crucial for designing efficient engines and braking systems.
Electronics
Circuits often contain circular components, such as printed circuit boards (PCBs) and circular conductive traces. Knowing the area of these elements aids in optimizing circuit design and ensuring proper functionality.
Geographical Mapping
Cartographers and geographers use the area of circles to represent and measure features on maps. This includes visualizing the extent of cities, marking the coverage area of national parks, or representing the distribution of population within circular regions.
Examples
Some examples of finding the area of a circle are as follows:
Example 1
The form of a big rope is round. It has a 10-unit radius. Find its Area?
Solution:
Step 1: Write a given data.
r = 10 units
π = 3.14
Step 2: As the rope is in a circular shape. So, we use a circular formula.
Area = π*r2
Step 3: Substitute the values in a given formula.
Area = (3.14) *(10)2
Area = (3.14) *(100)
Area = 314 units2
Example 2
If the circumference of the circle is 8 units. Calculate its area.
Solution:
Step 1: Write a given data.
C = 8 units
Step 2: Write the formula of the circumference.
C = (2π) *r
Step 3: Substitute the values and by using mathematical rules find the value of “r”.
8 units = (2π) *r
8 units = (2*3.14) *r
8 units = 6.28*r
8 units / 6.28 = r
1.27 units = r
Step 4: Write the formula of the area of a circle.
Area = π*r2
Step 5: Put the values.
Area = (3.14) *(1.27)2
Area = (3.14) *(1.6129)
Area = 5.06 units2
Example 3
Find the area of the circle if the radius is 21 cm.
Solution:
Step 1: Write a given data.
r = 21 cm
π = 3.14
Step 2: Write the formula.
Area = π*r2
Step 3: Substitute the values in a given formula.
Area = (3.14) *(21)2
Area = (3.14) *(441)
Area = 1384.74 cm2

