To calculate result you have to disable your ad blocker first.
Midpoint Rule Calculator
To use midpoint rule calculator, enter function, boundary points, subintervals, and click calculate button
Table of Contents:
Midpoint Rule Calculator
Midpoint rule calculator is used to find the approximate definite integral over the given interval.
What is the midpoint rule?
Midpoint rule, also known as the midpoint approximation. It is the numerical integration technique that approximates the area under the curve f(x) by dividing the interval into subintervals of equal length and evaluating the functional value at the midpoint of each subinterval.
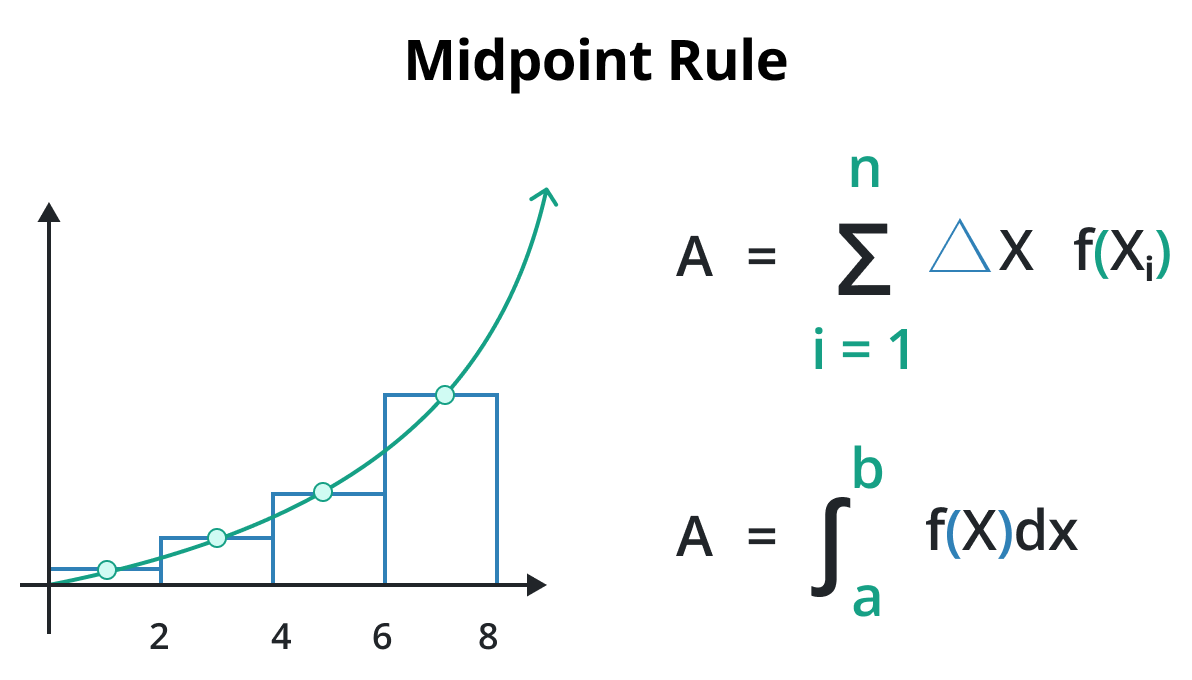
Formula
The formula of the midpoint rule of the given function is:
a∫bf(x) dx= Δx/2[f(x0+x1)/2+ f(x1+x2)/2+…+ f(xn-2+xn-1)/2+f(xn-1+xn)/2]
where Δx= (b-a)/n
- f(x) is the function whose midpoint is required.
- a and b are the lower limit and upper limit respectively.
- Δx is the length of the subinterval.
- x0,x1,x2 are the values of the subinterval.
Example
Find the midpoint of the function 2x2 - 3y where the upper limit is 3, the lower limit is 2 and the subinterval is 3.
Solution:
Step 1: The left Riemann sum rule for the endpoints:
a∫bf(x) dx= Δx/2[f(x0+x1)/2 + f(x1+x2)/2 +…+ f(xn-2+xn-1)/2 + f(xn-1+xn)/2]
We have that f(x) = 2x2-3y, a= 2, b= 3 and n=3
Therefore, Δx= (3-2)/3=1/3
Step 2: Find the subintervals
[2,3] interval is divided into n=3 subintervals of the length 1/3.
[2,7/3,8/3,3]
Step 3: Calculate the value
f(x0+x1)/2= f(2+7/3)/2 = f(13/6) = (169/18)-3y
f(x1+x2)/2= f(7/3+8/3)/2 = f(5/2) = (25/2)-3y
f(x2+x3)/2= f(8/3+3)/2 = f(17/6) = (289/18)-3y
Step 4: Now put all the values in the formula, we have
=1/3[(169/18)-3y+(25/2)-3y+(289/18)-3y]
=12.65-3y

