Modulo Calculator

This mod calculator is a mathematics tool that is used to find the remainder of a modulo b. The input boxes are labeled as divisor and dividend to make it easy to understand.

In this post, we will discuss what is mod and how to find it.

What is modulo?

Modulo is an operation used in mathematics. It is very similar to the remainder. In fact, the modulus is also known as the remainder operator.

Definition of modulo is:

“The modulo (or ''modulus” or ''mod”) is the remainder after dividing one number by another.”

Fun fact: Mod can be used to identify a number as even or odd. If x modulo 2 = 0 then, the number (x) is even. But if the mod is 1, the number is odd.

Mode is sometimes represented by the percent sign (%).

Modulo operator

The syntax of the modulo operator looks like this:

                          Dividend (a) mod Divisor (b) = C (remainder)     

This is an easy arrangement to understand. The modulus calculator above uses the same syntax. We will look at an example:

                                               7 mod 2 = 1

How did we know this? It is obvious that we divided 7 by 2.

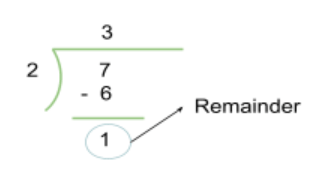
But dealing with mod, we are only concerned with the value of the remainder. We don’t need the value 3 that we get after the division.

To remove any confusion, see the difference between division expression and modulo expression.

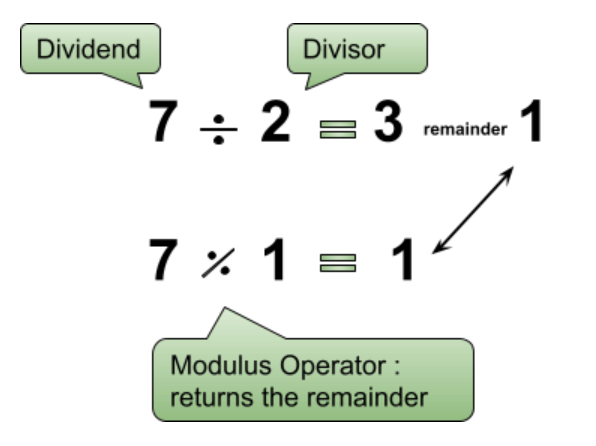
How to calculate modulo?

There are two ways to calculate modulo. The first one is the division method and the other one is clock arithmetics.

We will discuss the clock method later in the post but here is a trick to do the division method manually.

Example:

Consider you have to find the modulo of 14 mod 3.

Subtract 3 from 14. Then subtract 3 from its answer. Keep doing so until the answer is less than 3.

14 - 3 = 11

11 - 3 = 8

8   - 3 = 5

5   - 3 = 2

This means that 14 mod 3 = 2.

Now, on to the clock arithmetics. When 1 is constantly added to the dividend and divided by the same divisor we can see a pattern in the values of the remainder. For example:

Let’s take divisor 2. First, we will divide 0 by two, then 1 by 2, and so on.

0 mod 2 = 0

1 mod 2 = 1

2 mod 2 = 0

3 mod 2 = 1

4 mod 2 = 0

You can see the pattern 0, 1, 0,1 … for mod 2. Can you guess the pattern for mod 3?

It is 0,1,2,0,1,2 and so on. So it can be said that the pattern consists of Divisor-1 digits. If the divisor is 4 then the pattern is 0,1,2,3,0,1,2,3 … . Hopefully, you understood.

Now how can this information help to find mod?

We know that after twelve, the clock strikes one, and the circle starts again. If we replace 12 with 0, a clock will be a perfect example of mod 11. This is where the name clock arithmetics comes from.

Through this method, you can see what will be the remainder of different numbers for a particular mod. Let’s see an example.

Example:

What is the answer to 10 mod 3?

Solution:

The pattern of reminders is 0, 1, 2. We will build a clock for this pattern. Then we will start counting up to the number 10 and will determine at what digit of the pattern (0,1,2) it lies.

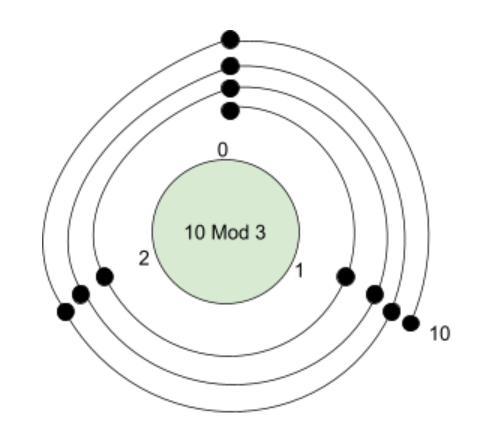
This drawing can help you know the remainder for other values with mod 3. For example, you can see that 6 lies at 0. This means 6 mod 3 = 0.You can see for yourself that if you start counting the whole numbers from 0 the number 10 will be at 1. This means 10 mod 3 = 1.

These are the two techniques used to find the mod. But to save time, use the modulo calculator.