Outlier Calculator

Outlier Calculator

Outlier calculator is an online tool that helps to analyze the datasets and find the outlier values. It sorts data from lower to higher outlier boundaries for easy understanding. 

This outliers calculator determines the outlier’s value using the IQR (Interquartile Range) method and outliers formula. It provides a detailed step-by-step solution to every problem. 

Outlier Definition 

Outlier is a data point that significantly deviates from the other data points in any data set. Outliers come due to the variability of data, measurement errors, or unusual occurrences. It is usually high or low compared to most of the values. 

Outliers have a significant impact on statistical analysis. It skews the results and helps to draw accurate conclusions. Therefore, it’s important to identify the accurate outlier values.

How to Find Outliers?

There are many manual methods to calculate outliers. These methods names and detailed are given below:

1. Interquartile Range (IQR) Method (Tukey’s Fences)
2. Z-score Method (Standard Score)
3. Sorting method
4. Using visualizations

1: Interquartile Range (IQR) Method (Tukey’s Fences)

The IQR method identifies outliers by calculating the difference between the data’s 1st quartile (Q1) and the 3rd quartile (Q3). For this use the outlier formula or Tuckey’s fences.

Tukey’s fences:

• lower outlier boundary  = Q₁ – 1.5 * IQR
• Upper outlier boundary  = Q₃ + 1.5 * IQR

Quartile:

• Q₁ = (1/4) * (n + 1)
• Q₃ = (3/4) * (n + 1)  

IQR (Interquartile Range) = Q₃ –Q₁

Identification of outliers depends on the result of the lower and upper outlier boundary. 

• If the data point below the result of the lower outlier boundary or lower fence is considered an outlier.
• If the data point above the upper outlier boundary or upper fence is considered outlier. 

2: Z-score Method (Standard Score)

The Z-score method is used to find the Z-score measures that tell the threshold value and select the outliers. Calculating the z-score value for each data using the z-score formula and outliers values depending on threshold. 

The common threshold is 3, which means a data point having a Z-score greater than 3 or less than -3 is considered an outlier. The z-score formula used to find the z-value is stated as:

Z = (X – μ) / σ

Where:

• X is the data point,
• μ is the mean,
• σ is the standard deviation. 

For z-score calculation, you can use our Z-score Calculator.

3: Sorting Method

In this method, first sort the numbers from ascending to descending order. This arrangement helps to show extremely low or high values. Outliers appear at the beginning or end of the sorted list. 

For Example: if the data is {60,40, 9,4, 6} then Sorting values from lowest to highest order. To arrange the lowest to highest order quickly use our least to greatest calculator.

4,6,9,40,60  

Bold values are outliers in given data.

4: Using Visualization

A great way to find outliers is to use a box-and-whisker plot calculator to visualize your data. It creates a chart highlighting the data range, median, and interquartile range. 

Outliers are typically represented outside the whiskers of the box plot. If data points are plotted beyond the whiskers, then it is known as potential outliers. In the below image, the points outside the whiskers (represented by dots) are potential outliers.

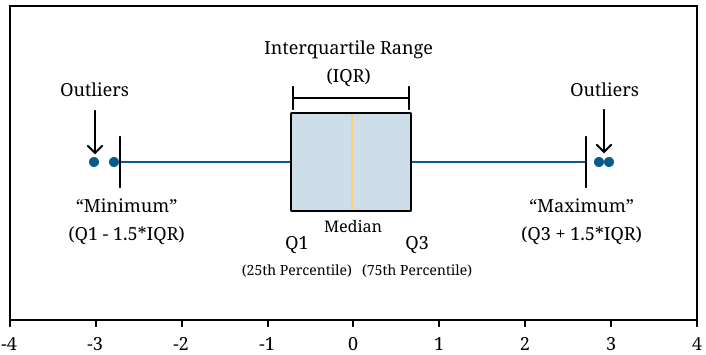
Outlier Examples

In this section, we will show the work of our online outlier calculator and clarify the understanding of the above methods by detailed steps. 

Example 1: Find the outliers of the given dataset using the interquartile range method:
{10, 15, 12, 18, 22, 20, 25, 30, 35, 28, 75}
Solution
Step 1: First, sort the dataset from least to smallest order.

Order Set = {10, 12, 15, 18, 20, 22, 25, 28, 30, 35, 75}

Step 2: Find the first Quartile (Q1). 

Q1 = (1/4) * (11 + 1)-term = 3-term

Note the 3rd term from ordered sets.

Q1= 15

Step 3: Evaluate the Quartile (Q3) Calculation:

Q3 = (3/4) * (11 + 1) = 9-term

The 9-term number is 30.      

Thus,                     Q3 = 30

Step 4: Find, the Interquartile Range by its formula.

IQR = Q3 - Q1

IQR = 30 - 15

IQR = 15

Step 5: Now find the Low and upper fence values by these formulas for outlier results.

Lower Fence = Q1 - (1.5 x IQR)

Lower Fence = 15 - (1.5 X 15) = -7.5

Upper Fence = Q3 + (1.5 x IQR)

Upper Fence = 30 + (1.5 X 15) = 52. 5

Thus,                     Outliers = 75

Example 2: Find the outlier using the Z-score Method the dataset of student test scores is given below:
[65, 70, 75, 80, 85, 90, 95, 100, 105, 50].

Solution

Step 1: Calculate Mean (μ) and Standard Deviation (σ)

Mean (μ) = (65 + 70 + 75 + 80 + 85 + 90 + 95 + 100 + 105 + 50) / 10 = 81.5
Standard Deviation (σ) ≈ 16.8

Step 2: Calculate Z-scores for each data point

Z = (X – μ) / σ

For example:

For 65: Z = (65 – 81.5) / 16.8 ≈ -0.98
For 50: Z = (50 – 81.5) / 16.8 ≈ -1.87
For 105: Z = (105 – 81.5) / 16.8 ≈ 1.40

Step 3: Identify Outliers

As discussed above any data point with a Z-score beyond ±3 is considered an outlier. By the z-score method, there is no outlier because all values lie in the range.
To verify the results of the above data use our above outlier calculator.

Frequently Asked Question

What is the main purpose of outliers?
The main purpose of Outliers by Malcolm Gladwell: “Explores the factors that contribute to high levels of success, such as opportunity, cultural background, and practice.”

Why do outliers occur?
Here are 4 more common causes of outliers in datasets:

• Changes in system behaviors
• Fraudulent Behavior
• Human Error
• Natural Deviations in Populations

Why is it important to identify outliers? 
Identifying outliers is essential because it skews the data analysis results and leads to inaccurate conclusions. Finding or addressing outliers helps ensure more accurate statistical insights, so we need to handle them carefully and appropriately. 

Can the Outlier Calculator handle large datasets? 
Yes, Our outlier calculator can evaluate every size or type of dataset such as test scores and financial data. Simply paste or enter the values separated by commas and the tool evaluates the outliers after pressing the button.

How to visualize outliers?
Visualize the outlier using a box plot or whisker plot, for this use the box plot calculator. The charts or box plots highlight Outliers, minimum and maximum values, median, and interquartile range.