To calculate result you have to disable your ad blocker first.
Pascal's Triangle Calculator
To use Pascal's triangle calculator, select the rows option, enter the number of rows, and hit calculate button
Pascal's Triangle Calculator
Pascal's triangle calculator is used to calculate Pascal’s infinite triangle of numbers with the help of binomial expansion.
What is Pascal’s triangle?
Pascal's Triangle is a fascinating mathematical concept that exhibits various patterns and has numerous applications in different fields. This triangular array of numbers, named after the French mathematician Blaise Pascal, unveils a multitude of intriguing properties that continue to captivate mathematicians and enthusiasts alike.
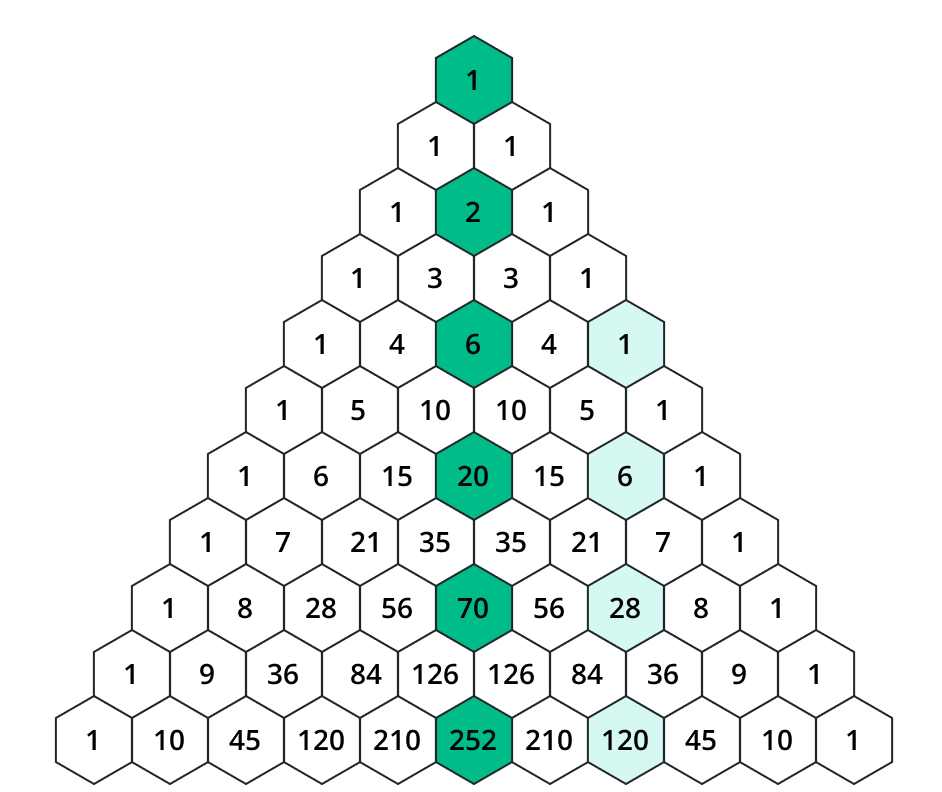
Understanding Pascal’s triangle:
Pascal's Triangle is an infinite triangular arrangement of numbers, starting with a single 1 at the top. Each subsequent row is constructed by adding the two numbers directly above it. The first few rows of Pascal's Triangle are as follows:
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
Up to infinity.
How to construct Pascal’s triangle?
Pascal's Triangle can be constructed by following a simple set of rules. The first and last element of each row is always 1, while the remaining elements are obtained by summing the two numbers above them.
The number in the nth row and kth column is denoted as C (n, k), representing the combination of choosing k elements from a set of n elements.
Patterns of a Pascal's Triangle:
Pascal's Triangle exhibits various intriguing patterns. Some notable patterns include:
- Each row corresponds to the coefficients of the binomial expansion of (a + b)n, where n represents the row number.
- The sum of each row is a power of 2.
- The diagonal elements of Pascal's Triangle represent the Fibonacci sequence.
Binomial Expansion and Pascal's Triangle
One of the significant applications of Pascal's Triangle is in the expansion of binomial expressions. Each row of Pascal's Triangle provides the coefficients for expanding a binomial raised to a specific power.
For example:
The coefficients of (a + b)3 are obtained from the fourth row of Pascal's Triangle: 1, 3, 3, 1.
Fibonacci Sequence and Pascal's Triangle:
Remarkably, the Fibonacci sequence can be derived from Pascal's Triangle. The sum of the diagonal elements of Pascal's Triangle represents the Fibonacci sequence, where each number is the sum of the two preceding numbers: 1, 1, 2, 3, 5, 8, 13, 21, and so on.
Alt text: Fibonacci sequence in terms of Pascal’s triangle.
Solved Example
Example
Construct a Pascal triangle from row 4 to row 10.
Solution:
The Pascal triangle for the given data is as follows:
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
1 9 36 84 126 126 84 36 9 1
1 10 45 120 210 252 210 120 45 10 1
Note: It is not necessary to draw a triangle outside the entries.

