To calculate result you have to disable your ad blocker first.
Ratios of directed line segments calculator
Enter points and ratio in the given input boxes and select the type of partition, i.e. internally or externally. Hit the calculate button to find the coordinates of point using partitioning a line segment calculator.
Partition calculator
Ratios of directed line segments calculator is an online tool that finds the point coordinates dividing the line (internally/externally) joining two points A and B for a given ratio m and n.
Coordinates of a point - Definition
Coordinates of a point are a pair of numbers that state its precise location on a two-dimensional plane. The coordinate plane has two axes at right angles to each other, called the x and y axis.
Formula of coordinates dividing a line segment
Coordinates dividing line internally
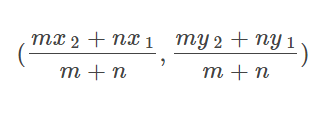
Coordinates dividing line externally

Where,
x1, x2, y1, y2 are end point of a line segment,
m and n are external and internal ratios.
How to find ratio of a directed line segment?
Let’s find out coordinates of points dividing a line segment joining two points with an example.
Example:
Find the point coordinates that divides a directed line segment internally having endpoints (2, 4), (3, 6) with a ratio of 5:6.
Solution:
Step 1: Identify the values.
x1 = 2, x2 = 3, y1 = 4, y2 = 6, m = 3, n = 1
Step 2: Place the values in equation of internal ratio of directed line segment.
= (mx2+nx1/m+n, my2+ny1/m+n)
= (3×3+1×2/3+1, 3×6+1×4/3+1)
= (11/4, 22/4)
Hence, the points (11/4, 22/4) divides the line joining points (2, 4), (3, 6) with a ratio of 5:6.
Use external ratio segment formula for external points coordinates or use our segment partition calculator above to automate your calculations.

