Quartile Calculator

Quartile Calculator

Quartile calculator is an online tool that can find:

• First Quartile (Lower)
• Median (2nd Quartile)
• Third Quartile (Upper)
• Interquartile Range (IQR)

In this post, you will learn about quartiles and how to find them.

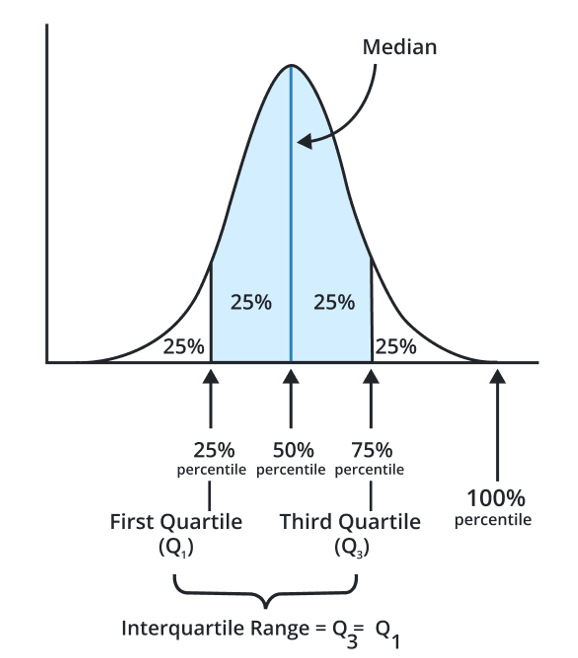
Quartiles - Definition

Quartiles are three such points that divide a group into four equal parts. Each quartile accounts for a separate fourth part.

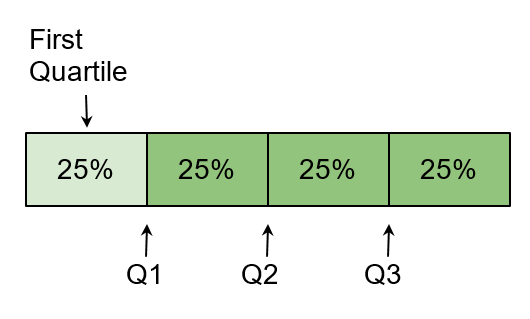
First Quartile (Q1)

It is the lower quartile which is the 25th percentile of the group. It is the point that divides the group in ratio 1:3.

Second Quartile (Q2)

It is the central quartile which is the 50th percentile of the data. It is the point that divides the group in ratio 2:2. It is also called the median.  

Third Quartile (Q3)

It is the upper quartile which is the 75th percentile of the group. It is the point that divides the group in ratio 3:1.

Note: A group is divided into 100 percentiles.

Quartile Formulas

There is a general quartile formula that is adjusted according to the need for calculating a particular quartile. This formula is:

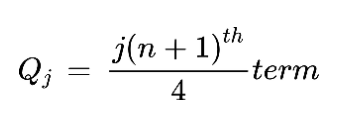
Where ’J’ is the number of quartile i.e 1,2,3.

Interquartile range formula

IQR = Q3 - Q1

Where Q3 and Q1 are third and first quartiles respectively.

How to find Quartiles?

Example

For the following set of data, find the 1st and 3rd quartiles. Also, find IQR.

3, 1, 6, 9, 12, 15, 18  

Solution:

Step 1: Arrange the values in ascending order.

1, 3, 6, 9, 12, 15, 18

Step 2: Put the values in the quartile formula for the first quartile.

Q1 = 1(n+1)^th/4 term

Q1 = 1(7+1)^th/4 term

Q1 = (8)^th/4 term

Q1 = 2nd term

2nd term is 3. So,

Q1 = 3

Step 3: Put the values in the quartile formula for the third quartile.

Q3 = 3(n+1)^th/4 term

Q3 = 3(7+1)^th/4 term

Q3 = 24^th/4 term

Q3 = 6th term

6th term is 15. So,

Q3 = 15

Step 4: Put these values in the interquartile formula or use the IQR calculator above.

IQR = Q3 - Q1

IQR = 15 - 3

IQR = 12