To calculate result you have to disable your ad blocker first.
Trapezoidal Rule Calculator
To calculate the approximated area, enter the function, upper limit, lower limit, and interval of the function using a trapezoidal rule calculator
Trapezoidal Rule Calculator
Trapezoidal rule calculator is a helpful resource for evaluating the approximated integral (area under the curve). This calculator takes the values of the lower and upper limits of the function with the interval to solve the output with steps
What is a trapezoidal rule?
The trapezoidal rule is a numerical method used to approximate the definite integral of a function. This method is based on the idea of approximating the region under the graph of the function as a trapezoid, instead of a rectangle, which is the basic idea behind the Rectangular Rule.
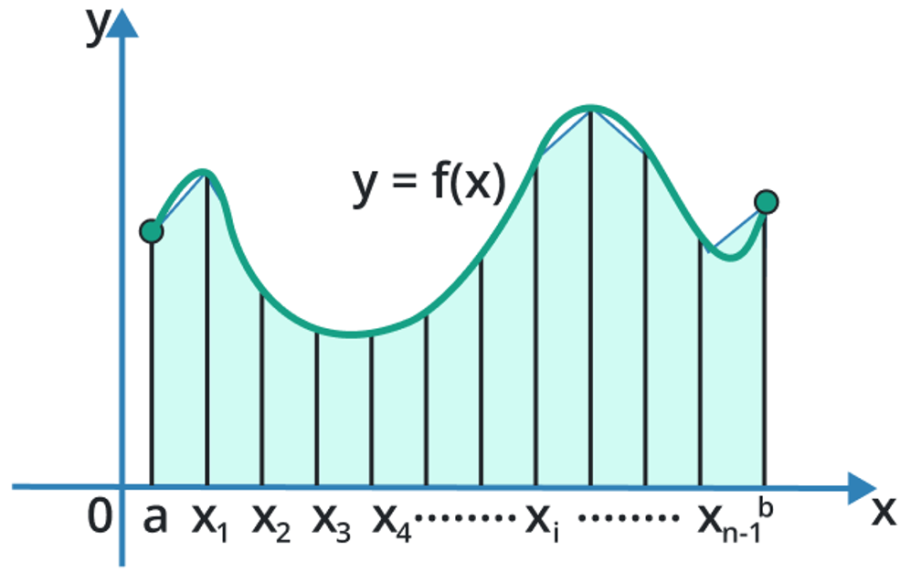
The Trapezoidal Rule provides a more accurate estimate of the definite integral than the Rectangular Rule, especially for functions that are not well approximated in a straight line.
Formula:
The general formula of the trapezoidal rule is given as:
$$\int _a^b\:f\left(x\right)dx=\frac{\Delta x}{n}\left[f\left(x_0\right)+2f\left(x_1\right)+f\left(x_2\right)+f\left(x_3\right)+...+f\left(x_{n-1}\right)+f\left(x_n\right)\right]$$
- f(x) is the function whose integral find.
- a and b are the limits of the function.
- x is the difference between the limit.
- n is the number of subintervals.
How to calculate definite integral by using trapezoidal?
The method of finding trapezoidal is explained briefly, in the below example.
Example:
Approximate the area under the curve of function f(x)= 2x^2-3x where the number of subintervals n=3 upper limit is 3 and the lower limit is 2.
Solution:
Step 1: Formula of the trapezoidal rule
$$\int _a^b\:f\left(x\right)dx=\frac{\Delta x}{n}\left[f\left(x_0\right)+2f\left(x_1\right)+f\left(x_2\right)+f\left(x_3\right)+...+f\left(x_{n-1}\right)+f\left(x_n\right)\right]$$
Where
Δx/2 = (b - a)/n
Step 2: The Subintervals are
Δx= (3-2)/3
Δx = 1/3
Divide the interval [2,3] into n=3 subintervals of the length x = 1/3 with the endpoints.
2, 7/3, 8/3, 3
Step 3: Now just evaluate the function at endpoints.
f(x0) = f(2) = 2
f(x1) = f(7/3) = 35/9
f(x2) = f(8/3) = 56/9
f(x3) = f(3) = 9
Step 4: Now sum up all the values according to the formula
= 1/6[2 + 2(35/9 + 56/9) + 9]
= 5.203
Hence the area under the given curve is 5.203

