Matrix Rank Calculator

Matrix Rank Calculator

Matrix rank calculator takes the value in a square order, after that according to the Gauss elimination method it converts all the non-diagonal elements equal to zero. In the end, it finds all the non-zero rows from the reduced matrix.

What is the rank of a matrix?

Maximum number of linearly independent rows or columns in a matrix is referred to as the matrix's rank. In other words, it is the size of the vector space that is covered by the matrix's rows or columns. 

Numerous techniques, including row reduction singular value decomposition, and counting the number of non-zero eigenvalues of the matrix, can be used to calculate the rank of a matrix.

How to calculate the rank of a matrix?

Example

Find the rank of the matrix

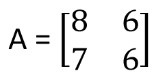
Solution:

Step 1: Augment the matrix with the identity matrix.

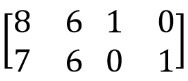
Step 2: Make zero in column 1 except the entry at row 1, column 1.

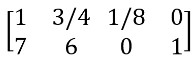
Step 3: Now make the zero below diagonal element 1.

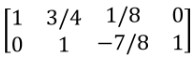
Step 4: Now the number of nonzero rows is two.

Hence, the rank of matrix A= 2.