To calculate result you have to disable your ad blocker first.
Arc Length Calculator
To find the arc length, enter the value of radius and angle in radians in the input boxes and hit the calculate button using this arc length calculator.
Arc Length Calculator
Arc length in radians calculator computes the arc length and other related quantities of a circle. These values include:
- Sector Area
- Chord
- Diameter
This tool also allows choosing the units of the input quantities because they are of significant importance when computing some value. The results are in the SI units.
What is the arc length?
The length along the curve of a circle between two points of its circumference. It depends on the central angle and the radius of the circle.
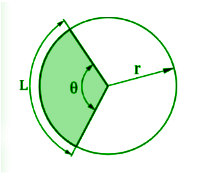
It is different from the chord of a circle because a chord is a straight line between two points while an arc is curved.
Visit our other circle-related tools e.g. Circumference and Circle area calculator.
Arc length formula:
Let’s derive the formula to find the length of an arc of any circle. As you may already know, for a 360 (2π) degrees angle, the arc length is equal to the circumference.
This means the proportion between these two values is constant.
L / θ = C / 2π
Where L is the arc length and theta is the central angle. Now, the circumference of a circle can be written as 2πr as well, right? So the proportion becomes:
L / θ = 2πr / 2π
L / θ = r
L = r * θ
This is the simplified formula of arc length. This formula is applicable when the central angle is given in radians. But if the angle is measured in degrees, then multiply the angle with π/180.
L = r * θ * π/180
L = r * π * θ/180
L = θ/180 * rπ
The arc length calculator can find the arc length in whichever unit you provide the angle e.g. arcminutes or pi radians.
How to find the arc length?
It is important to convert the units of the angle and radius in the SI unit. After that, multiply both values.
Example:
For a circle of 8 meters, find the arc length with the central angle of 70 degrees.
Solution:
Step 1: Write the given data.
Radius (r) = 8m
Angle (θ) = 70o
Step 2: Put the values in the formula.
Since the angle is in degrees, we will use the degree arc length formula.
L = θ/180 * rπ
L = 70 / 180 * (8)π
L = 0.3889 * (8)π
L = 3.111 * π
L = 9.774 meters
How to find arc length using sector area and central angle?
When the available data does not include the radius then it is possible to find the arc length using the sector area of the circle. The formula used is:
L = θ * √2A/θ
where A is the sector area. Follow these steps to use this formula.
- Multiply the sector area by 2.
- Divide this value by the angle.
- Now, take the square root of the value.
- Lastly, multiply with the angle again.
A solved example for this case is given below.
Example:
What will be the arc length if the sector area is 360000 cm2 and the angle is 60 degrees?
Solution:
Step 1: Convert the centimeters into meters and degrees to radians.
1 centimeter2 = 1/10000 meter square
360000 cm2 = 360000/10000 meter square
= 36 meter square
1 degree = π/180 radians
60 degrees = 60 * π/180 radians
= 1.0472 rad
Step 2: Write the available data.
Area (A) = 36 m2
Angle = 1.0472 rad
Step 3: Use the formula.
L = θ * √2A/θ
L = (1.0472) * √2 (36) /1.0472
L = (1.0472) * √72 /1.0472
L = (1.0472) * √75.3984
L = (1.0472) * 8.6832
L = 9.09 meters

