To calculate result you have to disable your ad blocker first.
Centroid of a Triangle Calculator
Input the three vertices of a triangle in the centroid of a triangle calculator to find the centroid.
Centroid Calculator
This online calculator finds the centroid of a triangle in 2 dimensions. It means you can compute the center point of the triangle known as a centroid.
What is a Centroid?
A centroid is a point where the three medians of a triangle intersect each other. If a polygon is fixed at its centroid, the figure becomes geometrically balanced.
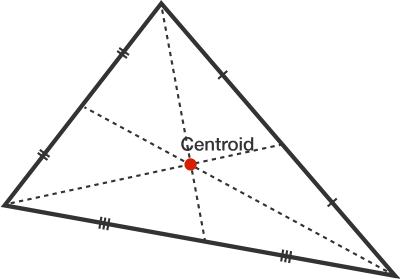
A very common mistake people make is that they think the centroid divides medians in half. Actually, the centroid is the point that divides medians in the ratio of 2:1.
Centroid of a Triangle Formula
The formulas of the centroid are different for polygons. The formula used to compute the centroid of a triangle is:
Centroid = X1 + X2 + X3 / 3 , Y1 + Y2 + Y3 / 3
It is very similar to the formula of the midpoint. It is important to note that the answer is in the form of a point.
How to calculate the Centroid of a Triangle?
Example:
The points A, B, and C of a triangle are (1,2), (2,3), and (3,1) respectively. Find the centroid of this triangle.
Solution:
Step 1: Write all the vertices.
X1 = 1 , Y1 = 2
X2 = 2 , Y2 = 3
X3 = 3 , Y3 = 1
Step 2: Add all the X vertices and Y vertices.
= X1 + X2 + X3 , Y1 + Y2 + Y3
= 1 + 2 + 3 , 3 + 2 + 1
= 6, 6
Step 3: Divide both sums by 3.
= 6/3 , 6/3
= 2, 2
Hence, the centroid of this triangle exists on point (2,2) on the cartesian plane.

