To calculate result you have to disable your ad blocker first.
Imaginary Number: Definition, Properties, and Examples

Publish Date: 08 Aug, 2023
Table of Content
As we, all know that the square of a real number is non-negative. So the solution of the equation x2 + 1 = 0 or x2 = –1 does not exist in R. We need a number whose square is equal to a negative one. To overcome this limitation of real numbers, mathematicians introduced a set of complex numbers containing R and every number whose square is negative. They invented the imaginary number i (iota). They invented the imaginary number i (iota), equal to a negative one. By taking the new number i = - 1, the solution set of x2 + 1 = 0 is {i, -i}.
This article will discuss the definition, properties, and application of imaginary numbers. With the help of examples, we will learn how to solve any imaginary number.
What is an Imaginary Number?
Imaginary numbers are numbers that can be expressed as the square root of negative numbers. In other words, imaginary numbers are multiples of the imaginary unit, denoted by ‘i’. Where ‘i’ expresses the square root of -1.
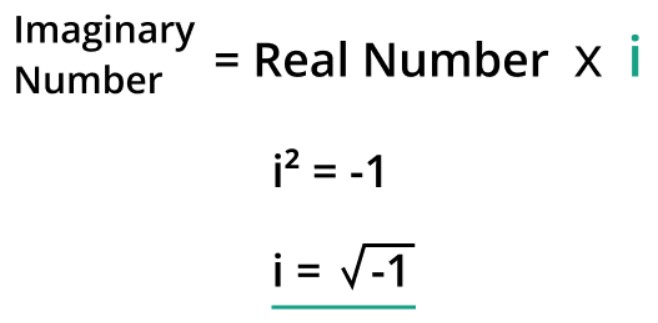
Imaginary numbers cannot be represented on an ordinary number line. They exist in a separate dimension called the imaginary plane. In the imaginary plane, the horizontal axis represents the real part of a complex number, and the vertical axis indicates the imaginary part.
Imaginary numbers are written in the form of ‘ix’. Here ‘x’ is a real number and ‘i’ is the imaginary unit. It is important to note that when ‘x’ equals zero, the number becomes real. 2i, and -5i are examples of imaginary numbers.
What is complex numbers?
Complex numbers are made up of the combination of real and imaginary numbers with the addition or subtraction operation. The number in the form x + iy is called a complex number. Where x is called the real and y is called the imaginary part. Note that every real number is a complex number with o as its imaginary part.
Following are some examples of complex numbers and imaginary parts:
Complex numbers | Real part | Imaginary part |
-2 + 4i | -2 | 4 |
0 + 9i | 0 | 9 |
-7i + 5 | 5 | -7 |
5 - 3i | 5 | -3 |
Imaginary Numbers Properties
Here are some notable properties of imaginary numbers:
- i2 = -1
The most fundamental property of imaginary numbers is that their square is equal to -1. This property serves as the basis for many calculations involving imaginary numbers.
- Addition and Subtraction
We treat the real and imaginary parts separately for adding and subtracting.
For example, (3 + 2i) + (1 - 4i) = (3 + 1) + (2 – 4) i = 4 - 2i.
- Multiplication
We can apply the distributive property to the product of two imaginary numbers. For instance, (2i) (3i) = 6i^2 = -6.
- Division
Multiplication of the numerator and denominator by the conjugate of the denominator is used to divide complex numbers. This process helps eliminate the imaginary part from the denominator.
Applications of Imaginary Numbers
While imaginary numbers may seem abstract, they have practical applications in various fields. Here are some of these applications:
Electrical Engineering
Imaginary numbers play a crucial role in analyzing and designing electrical circuits. They help represent alternating current (AC) signals and facilitate calculations involving phase shifts and impedance.
Quantum Mechanics
Imaginary numbers are used in quantum mechanics to describe physical phenomena at the atomic and subatomic levels. They enable the formulation of Schrödinger's equation and provide a mathematical framework for understanding wave-particle duality.
Signal Processing
Imaginary numbers find applications in signal processing, where they help analyze and manipulate complex waveforms. They are particularly useful in Fourier analysis, which decomposes signals into their constituent frequencies.
Euler's Formula
Euler's formula establishes a deep connection between trigonometry, complex numbers, and imaginary numbers. It states that e iθ = cos (θ) + i sin (θ), where "e" represents Euler's number and "θ" is an angle in radians. This formula beautifully relates the exponential function, trigonometric functions, and imaginary numbers.
Computer Graphics
Imaginary numbers are used in computer graphics to represent rotation and scaling.
Examples
Example 1
Evaluate the imaginary number i50.
Solution:
Given: i50
Step 1: Write the i50 in an exponent of 2 as:
i50 = (i2)25
Step 2: as we know, i2 is equal to -1. Substitute the value of i2
= (-1)25
Step 3: After simplifying it, we get
(-1)25 = -1
Therefore, i50 = -1.
Example 2
Simplify 1 / -i
Solution:
Given
= 1 / -i
Step 1: Multiply the numerator and the denominator by the conjugate of -i, which is i.
(1 / -i) × (i / i) = (1 × i) / (-i × i)
Step 2: Simplify the above expression:
i / (-i × i) = i / (-i2)
Step 3: Apply the property that i2 is equal to -1:
i / (-(-1)) = i / 1 = i
Therefore, the expression 1 / -i is equal to i.
Conclusion
In this article, we have discussed the definition, properties, and applications of imaginary numbers. We also explained the complex number with examples. Now you can grab all the basics of this topic from this platform.

