Square Root Calculator

Square Root Calculator 

Square root calculator eliminates the effort of dividing digits to find the roots. Find both perfect and imperfect square roots using the square root simplifier. 

What is square root?

The square root of a number A finds a number B that on multiplying by itself again gives the number A. In mathematical form:

                                  √X = Y where Y * Y = X 

There are other ways to define square root as well. It can be defined in fraction and exponent form as:

                                   X^1/2 = Y where Y² = X

The square root of a number gives two values: the exact number but opposite signs. For example, the square root of 4 is +2 and -2. The +2 is called the principal square root. 

If a number is the area of a square then its square root will give the measurement of its one side. Similarly, the backward calculation gives the area of the square.  

There are two types of square roots; perfect and imperfect. The perfect square root is a value that solves to a whole number like √16 = 4 while an example of an imperfect square root will be √15 = 3.87.

How to find the square root?

Usually, scientific calculators come with the square root operation button. But if you don't have access to a calculator, you can always use the online square root simplifier. 

It is possible to calculate the square root by hand but the methods are time-taking. The four ways to find the square root of a number are:

• Subtraction method
• Long division
• Trial and error method
• Prime factorization method

Subtraction Method

In the first method, subtract the odd numbers in sequence from the value until 0 remains. The number of times subtraction is done will be the square root. It is only applicable to perfect squares. 

Example:

To solve 25 using this method, firstly, subtract 1 from it.

25 - 1 = 24
24 - 3 = 21
21 - 5 = 16
16 - 7 = 9
9 - 9 = 0

The total number of subtractions done is 5 and this is the square root. 

Long Division

The second method is the long division. It is a little different from the usual division. Start by dividing with the largest possible digit. For the next step, add that radical coefficient to itself and place the quotient value next to it. 

If the radical coefficient consists of two digits, then add the digit at the smaller place value. 

Divide using this new number and repeat until you get zero or no more division is possible.

Example:

This one is an example of the imperfect square which also proves that this method can solve imperfect squares. 

Trial and Error Method

The third method is called the trial and error method. It is used in many mathematical calculations but is often skipped as it takes a lot of time. Also, you have to learn the perfect squares to use this.

Basically, you have to guess the value. You see what two perfect square roots it lies between. Like 10 is between 9 and 16. So its square root must be somewhere between 3 and 4. 

Then you notice which value is near. In our example, 10 is nearer to 9 than 16. So, it might be 3.1 or 3.2. Take the square and check. 

The square of 3.1 is 9.61 and that of 3.2 is 10.24. More accuracy can be achieved by guessing the next decimal place. Let's say it is 3.15 or 3.16 or 3.17. Taking squares of all three we have:
9.9225, 9.9856, and 10.0487. Let’s try to find one more time. What about 3.162 and 3.163. Their squares are 9.998244 and 10.004567. Both are very close to 10.  

Prime Factorization

The fourth and last method is called prime factorization because the factors of the number are calculated to get its square root. It is also used for perfect squares only. 

The factors are selected in pairs and solved. 

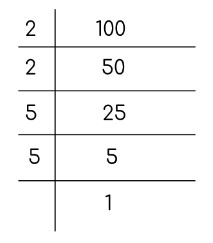
= 2 x 2 x 5 x 5
= 2² x 5²
= (2 x 5)²
= (10)²

So the square root of 100 is 10.