To calculate result you have to disable your ad blocker first.
Cone Calculator
To find the volume of cone, input radius (r) & height (h) and press the calculate button using cone calculator
Table of Contents:
Cone Calculator
Cone calculator is used to find the volume and slant height of the cone. This calculator also calculates the cone's total surface area as well as its curved surface area.
What is the Cone?
A cone is a three-dimensional object with a base that is circular and looks like a solid. From one end to the other, it gets smaller until it reaches its vertex. A right-angled triangle is used around one of the cone's sides to create it.
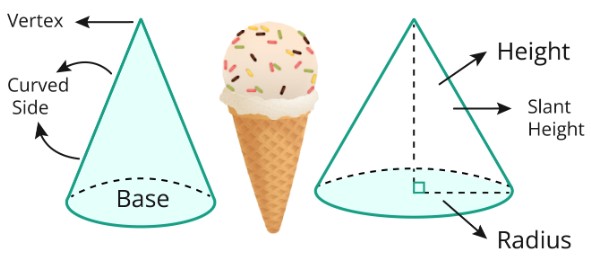
Some characteristics of a cone are given below.
Base of cone
A cone's base is a circular structure that is usually flat or rounded. One can determine the cone's base area and perimeter using the base diameter/radius.
Apex/Vertex of cone
The opposing end of a cone's base is known as the apex/vertex. It is a single point that is formed by the convergence of the sides of the cone.
Height of cone
The perpendicular distance between a cone's base and apex determines its height. It produced the cone's overall height.
Slant height of cone
It is the distance along the cone's diagonal from the apex to a point on its curved surface. It is shorter than the height and is calculated using the Pythagorean Theorem.
Formulas of Cone
- Volume (v) of Cone = (1/3)[πr²h]
- Slant Height (l) of Cone = l = [√(r² + h²)]
- Total Surface Area (TSA) of Cone = [πr(l+r)]
Where
- l = slant height of the cone
- h = height of the cone
- r = radius of the cone
Examples of Cone
Example 1
Find the volume (v) of the cone if its height is 36 and the radius of the base is 16.
Solution:
Step 1: Write the given values
h = 36, r = 16, V =?.
Step 2: Take the formula to find the volume of a cone.
Volume (v) of Cone = (1/3)[πr²h]
Step 3: Put the value in the above formula.
Volume (v) of Cone = (1/3)[π(16)2(36)]
Volume (v) of Cone = 9646.0000
Example 2
If the values of length and height are given as “r = 10, h = 42” then Calculate the volume of the cone, slant height, and total surface area of the cone.
Solution:
Step 1: Write the given values
h = 42, r = 10, V =?, l =?, total surface area =?.
Step 2: Take the formula of volume, slant height, and total surface area of a cone.
Volume (v) of Cone = (1/3)[πr²h]
Slant Height (l) of Cone = l = [√(r² + h²)]
Total Surface Area of Cone = [πr(l+r)]
Step 3: Put the value in the above formulas.
For Volume
Volume (v) of Cone = (1/3)[π(10)²(42)]
= 4396.0000
For Slant Height
Slant Height (l) of Cone = l = [√(r² + h²)]
= [√((10)² + (42)²)]
=1764.0000
For Total Surface Area
TSA of Cone = [πr (l+r)]
= [π (10){(1764)+(10)}]
= [π (10){(1764)+(10)}]
= [π (10){1774}]
= 55731.8537

