Pythagorean Theorem Calculator

Pythagorean Theorem Calculator

Pythagorean Theorem Calculator is a geometry assistant tool. It uses Pythagoras’ formula to find the three sides of a right triangle. You can find the hypotenuse or any of the other two sides.

How to use the Pythagoras theorem calculator? 

Follow the steps given below.

1. Choose the side of the triangle you want to find e.g. hypotenuse. 
2. Enter the value of the other two sides.
3. Click calculate.
4. The result will appear in a second.

You can use it multiple times for free by resetting the calculator.

What is the Pythagorean theorem?

The word Pythagorean comes from a famous Greek scientist Pythagoras who proved this theorem for the first time. It states that:

“The area of the square whose side is the hypotenuse (the side opposite the right angle) is equal to the sum of the areas of the squares on the other two sides.”

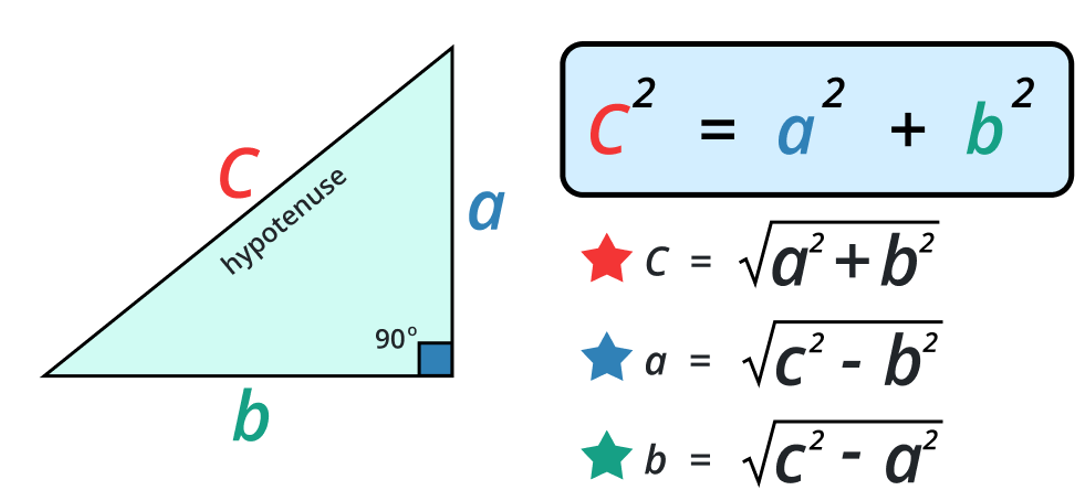
It can be used to derive the hypotenuse equation in which the hypotenuse is equal to the under-root of the sum of the squares of the other two lengths. It is written as:

c2 = a2 + b2 

Where c is the longer side opposite to the right angle known as hypotenuse. The letter a usually represents the adjacent side and the letter b represents the other side.

This equation is also known as the Pythagorean equation.

Formulas for the three sides from the Pythagorean equation

The equation can be arranged to find the length of any side.

• For hypotenuse: √(a2 + b2)

• For side a: √(b2 - c2)
• For side b: √(a2 - c2) 

Finding sides using the Pythagoras theorem

It never hurts to see an example, does it!?

Example:

Find the missing side for the following triangle.

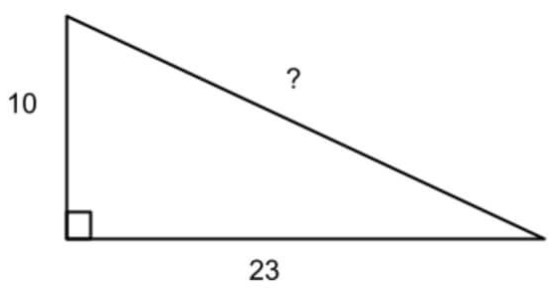
Solution:

Step 1: Identify the given data.

a = 10

b = 23

Step 2: Put in the Pythagorean equation.

c2 = a2 + b2

c² = (10)² + (23)²

c² = 100 + 529

c2 = 629

Step 3: Take square roots on both sides.

c = √629

c = 25.1