What is a Triangle? Types, properties, Examples

Triangles are one of the simplest and most versatile shapes in geometry, forming the basis for many other geometric concepts. A triangle is a fundamental geometric shape composed of three-line segments that intersect at three distinct points.

This article aims to cover the definition, types, properties, formulas for calculating area & perimeter, and examples of triangles.

What is a Triangle?

A triangle is a closed two-dimensional shape with three straight sides and three interior angles. The sum of the interior angles of a triangle always equals 180 degrees. The points of a triangle are called vertices, while the line segments are the sides of the triangle.

Tringles are classified based on sides and angles:

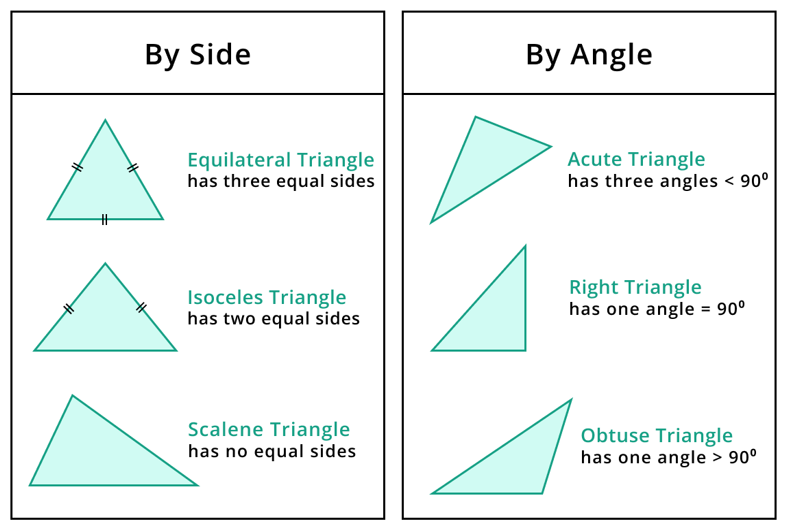
Types of Triangles: Based on Side Lengths

1. Equilateral Triangle.
2. Isosceles Triangle.
3. Scalene Triangle.

Equilateral Triangle

The lengths of the three sides are equal in an equilateral triangle. Each of its angles is 60 degrees. It is a special case of an acute triangle (all angles less than 90 degrees).

Isosceles Triangle:

An isosceles triangle has two sides of equal length and one side of a different length. The angles opposite the equal sides are also equal in measure. The angle opposite the longer side is typically larger than the other two angles.

Scalene Triangle:

A scalene triangle has all three sides of different lengths. Since its sides are unequal; its angles are also unequal. It can be an acute; obtuse; or right triangle; depending on the measures of its angles.

Types of Triangles: Based on Angle Measurements

Triangles can also be classified based on the measurements of their angles.

1. Acute Triangle:
2. Obtuse Triangle:
3. Right Triangle:

Acute Triangle:

An acute triangle has all three angles less than 90 degrees. In other words, all its angles are “acute” (smaller than a right angle).

Obtuse Triangle:

An obtuse triangle has one angle greater than 90 degrees; known as an “obtuse” angle. The other two angles are acute (smaller than 90 degrees).

Right Triangle:

A right triangle has one angle exactly equal to 90 degrees; which is known as a “right” angle. The sum of the other two angles is also 90 degrees.

Combined Classification

These two classifications can be combined to describe triangles more precisely:

• Equilateral Acute Triangle:

All sides are equal in length, and all angles are < 90 degrees.

• Isosceles Obtuse Triangle:

Two sides are equal in length; one angle is > 90 degrees.

• Scalene Right Triangle:

All sides are of different lengths; one angle is exactly 90 degrees.

Properties of Triangles

Triangles possess a range of properties. Some of the key properties include:

• Angle Sum Property: The sum of the three interior angles of a triangle always adds up to 180 degrees.
• Exterior Angle Property: The exterior angle of a triangle is equal to the sum of its two non-adjacent interior angles.
• Pythagorean Property: In a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides.

Area and Perimeter of a Triangle

The Perimeter of a Triangle:

The perimeter of a triangle is the sum of the lengths of all its sides.

P = a + b +c

Area of a Triangle:

Here are a couple of common methods to calculate the area of a Triangle:

Using Base and Height:

If you know the length of the base (b) of the triangle and its corresponding height (h) – the perpendicular distance from the base to the opposite vertex, then the area (A) can be calculated using the formula:

Area = 1/2 × Base × Height

The perimeter and area of a triangle can be solved by using our triangle calculator to get results in a fraction of a second.

Heron's Formula:

If you know the lengths of all three sides of the triangle you can use Heron's formula to calculate the area. Let “s” be the semi-perimeter of the triangle (half of the perimeter):  

S = a + b + c / 2

So, the area can be calculated using Heron's formula:

A = [s×(s−a) ×(s−b) ×(s−c)]1 / 2

Examples of Triangle:

Let’s solve some examples to gain more understanding of the triangle to solidify our understanding.

Example 1: Perimeter Calculation

Find the perimeter of a triangle with the following side lengths:

• Side a = 12 units
• Side b = 15 units
• Side c = 18 units

Solution:

To find the perimeter of a triangle with the given side lengths, simply add up the lengths of all three sides:

Perimeter (P) = Side a + Side b + Side c

Perimeter (P) = 12 units + 15 units + 18 units

Perimeter (P) = 45 units

Therefore, the perimeter of the triangle is 45 units.

Example 2: Area Calculation using Base and Height

Given a triangle with

base (b) = 16 units

height (h) = 9 units,

Calculate its area.

Solution:

To calculate the area of the triangle using the given base and height, you can use the formula:

Given:

base (b) = 16 units

height (h) = 9 units

Formula:

Area (A) = 0.5 × base × height

= 0.5 × 16 × 9 = 72 square units.

Example 3: Heron's Formula for Area

A triangle has side lengths:

• Side a = 7 units
• Side b = 9 units
• Side c = 12 units

Calculate the area of the triangle using Heron's formula.

Solution:

All three sides are available so we use Heron's formula.

Step 1: Find the perimeter

S = a + b + c / 2

S = (7 + 9 + 12) / 2

S = 28 / 2 s = 14 units

Step 2: Plug the values into Heron's Formula

Area = √ (s × (s - a) × (s - b) × (s - c))

Area = √ (14 × (14 - 7) × (14 - 9) × (14 - 12))

Area = √ (14 × 7 × 5 × 2)

Area = √ (980) Area ≈ 31.30495 square units

Therefore, the area of the triangle is approximately 31.30495 square units.