To calculate result you have to disable your ad blocker first.
Introduction to Geometry: Definition, Types, & Examples

Publish Date: 23 Nov, 2023
Table of Content
Geometry is the most significant and core dimension of mathematics that deals with the distinctive characteristics of figures in their plane, space, etc. It is the Greek word comprising "geo" and "metron" implying “land” and "measurement" respectively. It is historically an old field in mathematics.
Geometry highlights the longstanding connection between land measurement and building construction in earlier times. Understanding space and the nature of bodies is geometry. It demonstrates the underlying concepts guiding the geometric shapes that surround us and assists in our comprehension of their characteristics and interactions.
In this article, we’ll discuss the concept of geometry along with its main branches as well as some of its key applications.
What is Geometry?
A fundamental branch of mathematics that focuses on the relations and properties of surfaces, points, solids, and lines in space is known as geometry. It involves the study of sizes, shapes, and the relative positions of different figures, as well as the properties of space.
In geometry, we explore various geometrical objects, which include not only points and lines (such as segments and rays) but also curves (including those defined by functions), angles, and a range of surfaces and three-dimensional solids.
Branches of Geometry
The field of geometry can be broadly categorized into two main branches: plane geometry and solid geometry.
- Plane Geometry
- Solid Geometry
Plane Geometry (2D Geometry)
Plane geometry is concerned with the characteristics and relationships between geometric objects in a two-dimensional plane that can be drawn on a piece of paper. This area of study covers points, lines, angles, triangles, circles, polygons, and transformations like translations, rotations, reflections, and dilations.
Plane geometry provides the foundation for numerous additional disciplines of mathematics and is used extensively in computer graphics, architecture, engineering, art, design, and navigation.
The following are some key terms in plane geometry:
- Point
- Line
- Angles
Point:
On a plane, a point is an exact position or spot. Usually, a dot stands in for them. It is important to note that a point is a place rather than an object. Moreover, a point just has a position and it has no dimensions.
Line:
The line is thin, straight, and continuously long in both directions. It also has no bends, twists, or turns. It is crucial to remember that a line is made up of an unlimited number of points together. The terms "x-axis" and "y-axis" refer to the horizontal and vertical lines in geometry, respectively.
If a line has endpoints in both directions it is known as a line segment and if a line has only one endpoint then it is known as a ray.
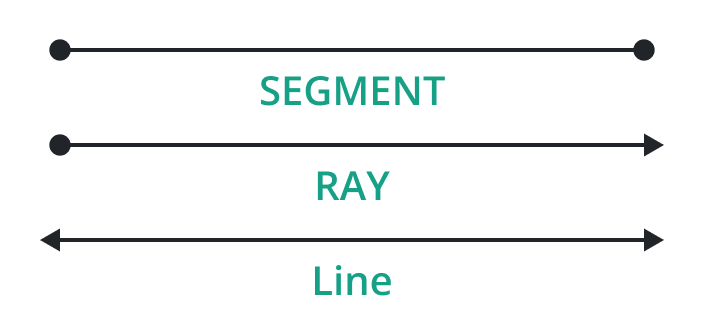
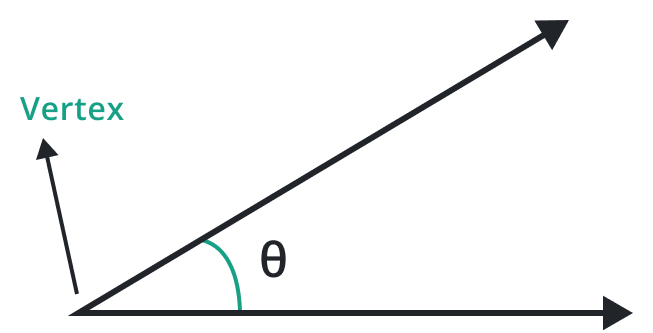
Angle:
An angle is a figure or shape made up of two rays that meet at a point known as the vertex of the angle in plane geometry and these rays are known as the sides of the angle sharing a common endpoint. A measurement expressed as a degree or radian between two rays is called an angle.
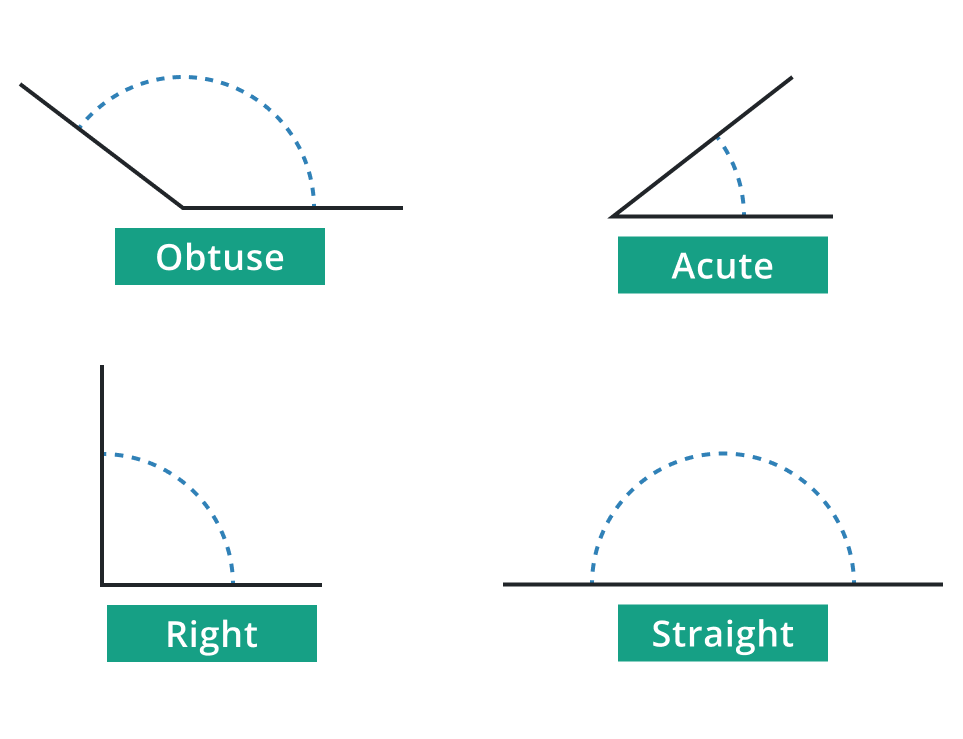
Types of Angles:
Acute Angle:
An angle (θ) is an acute angle if θ < 900.
Obtuse Angle:
An angle (θ) is an obtuse angle if θ > 900.
Right Angle:
An angle is a right angle if θ = 900.
Straight Angle:
An angle is called a straight angle if θ = 1800.
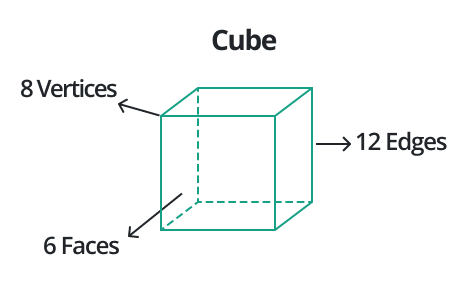
Solid Geometry (3D Geometry)
Studying three-dimensional objects is the subject of solid geometry in Euclidean space, commonly referred to as three-dimensional geometry. It encompasses apprehending the properties and relationships of complicated solids like prisms, pyramids, cylinders, cones, spheres, and others in three dimensions. Anyhow some solid shapes have no faces i.e. spheres.
Solid geometry is employed in architecture, engineering, manufacturing, computer-aided design (CAD), and 3D modeling. The important key terms of three-dimensional shapes are discussed here in the following:
- Edges
- Faces
- Vertices
Edges:
The line segment on the boundary that connects one vertex to another vertex is called an edge. It indicates that it connects two corner points. It creates a 3D-shaped skeleton. In other words, an edge is a set of faces that meet in a straight line.
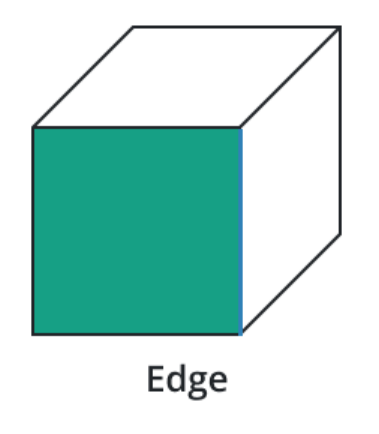
The list of edges for the various solid forms is as follows:
Solid Shapes | Number of Edges |
Cube | 12 |
Rectangular Prism | 12 |
Pentagonal Prism | 15 |
Hexagonal Prism | 18 |
Triangular Prism | 6 |
Square Pyramid | 8 |
Pentagonal Pyramid | 10 |
Hexagonal Pyramid | 12 |
Triangular Pyramid | 6 |
Faces:
In geometry, faces/flat surfaces are fundamental components of many structures. A flat, 2-D area enclosed by boundaries is known as a face. In 3-D shapes, each face itself is a 2-D figure. Understanding faces is essential for comprehending the structure and properties of both 2-D and 3-D geometric figures.
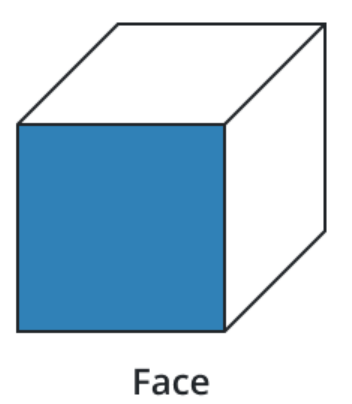
The following is a list of the number of faces for various solid shapes:
Solid Shapes | Number of Faces |
Cube | 6 |
Rectangular Prism | 6 |
Pentagonal Prism | 7 |
Hexagonal Prism | 8 |
Triangular Prism | 5 |
Square Pyramid | 5 |
Pentagonal Pyramid | 6 |
Hexagonal Pyramid | 7 |
Triangular Pyramid | 4 |
Vertices:
The point where the edges of a solid shape meet is called a vertex. In the context of a polygon, a vertex is the joining point of two neighboring sides. The intersection of the edges is known as the vertex.
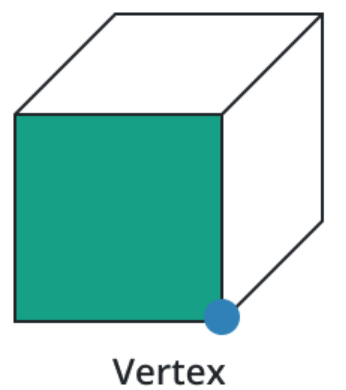
In geometry, a solid shape's number of vertices is as follows:
Solid Shapes | Number of Vertices |
Cube | 8 |
Rectangular Prism | 8 |
Pentagonal Prism | 10 |
Hexagonal Prism | 12 |
Triangular Prism | 6 |
Square Pyramid | 5 |
Pentagonal Pyramid | 6 |
Hexagonal Pyramid | 7 |
Triangular Pyramid | 4 |
Examples:
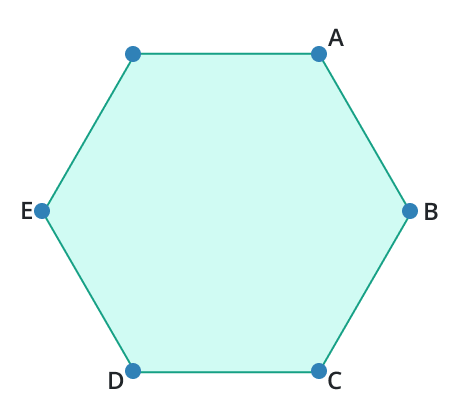
- What is the number of vertices in a hexagon?
Solution:
A polygon with six sides is known as a hexagon. According to the definition, in any polygon, the number of sides is equal to the number of vertices. Therefore, a hexagon has six vertices. The vertices of a hexagon are the points where its sides meet.
- Without counting, what is the number of vertices in a hexagonal pyramid?
Solution:
Number of vertices of pyramid = 1 + base’s vertices
The base of a hexagonal pyramid will be a hexagon.
So, the number of vertices of a hexagonal pyramid = 1 + hexagon’s vertices = 1 + 6 = 7
- What is the number of edges, faces, and vertices in a cube?
Solution:
By observing the shape of a cube, it has 12, 6, and 8 edges, faces, and vertices respectively.