To calculate result you have to disable your ad blocker first.
Covariance Calculator
Input comma-separated values of set x & y and hit the calculate button to find covariance
Table of Contents:
Covariance Calculator
Use the sample covariance calculator for a detailed calculation of the relation between two data sets. This covariance calculator will find the means of both data sets. The table included in the result area contains all the necessary values.
What is covariance?
Covariance in statistics describes the relation between two variables or data sets to see if the change in one affects the other. But the measure of this relation is found by correlation.
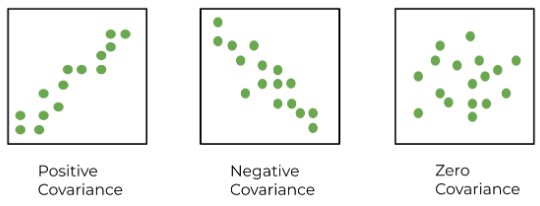
Covariance can be positive, negative, or zero.
- A positive covariance means both are directly related.
- A negative covariance indicates an indirect relation.
- A zero covariance tells both variables are independent of the changes in each other.
Covariance formula
To find the covariance, the following formula is used:
$$Cov_{x,y}=\frac{\sum \:\:_{i=1}^n\left(\left(x_{i\:}-\:x̄\right)\left(y_i\:-\:ȳ\right)\right)\:\:}{N-1}$$
- Covx,y is the covariance
- xi is the data set of x
- yi is the data set of y
- x̄ & ȳ are the mean of the x and y data sets respectively.
- N is the total numbers in the data set of x & y.
In this equation, the bar (-) above x and y is used to represent the mean.
How to find covariance?
Calculating covariance is a long process. Several values need to be calculated.
Below are the important steps.
- Find the mean of both data sets.
- Subtract the individual entries from the respective means of data sets.
- Multiply x1 with y1, x2 with y2, and so on after subtraction from the mean.
- Add all the values.
- Divide by the total number of values minus one (n-1).
Example:
Find the covariance for the given data sets.
X = 12, 13, 14, 15, 15, 18, 11, 12
Y = 20, 11, 12, 15, 11, 13, 12, 17
Solution:
Step 1: Find the mean of both sets.
Mean of X = 12 + 13 + 14 + 15 + 15 + 18 + 11 + 12
= 110 / 8
= 13.75
Mean of Y = 20 + 11 + 12 + 15 + 11 + 13 + 12 + 17
= 111 / 8
= 13.875
Step 2: Subtract and multiply as explained.
| xi | xi - ͞x | yi | yi - ͞y | (xi - ͞x) (yi - ͞y) |
12 | - 1.75 | 20 | 6.13 | -10.73 |
13 | -0.75 | 11 | -2.88 | 2.16 |
14 | -0.25 | 12 | -1.88 | -0.47 |
15 | 1.25 | 15 | 1.13 | 1.41 |
15 | 1.25 | 11 | -2.88 | -3.60 |
18 | 4.25 | 13 | -0.88 | -3.74 |
11 | -2.50 | 12 | -1.88 | 5.17 |
12 | -1.5 | 17 | 3.13 | -5.48 |
Step 3: Add these values.
= (-10.73) + 2.16+ (-0.47) + 1.41+ (-3.60) + (-3.74) + 5.17 + (-5.48)
= 15.28
Step 4: Use the covariance formula.
Cov( x,y) = ∑ (xi - ͞x ) (yi -͞y ) / n-1
= 15.28 / 8 -1
= 15.28 / 7
= -2.18
The number shows a negative covariance. Use our sample covariance calculator to cross-check the above result.
References
- Covariance. Corporate Finance Institute. (2022, November 4).

