To calculate result you have to disable your ad blocker first.
Cross Product Calculator
Select the dimensions, choose the vector representation, input the i, j, and k unit vector values, and click Calculate using cross product calculator
Cross Product Calculator
Cross product calculator is used to find the product of two vectors using the matrix method. The vectors can be entered using the coordinates representation or points.
It provides an option for choosing dimensions. This means you can find the product of vectors present in the i, j, and k dimensions on this cross-product calculator i.e. 3-D vectors.
Last but not least, this tool provides all the steps taken in the vector product computation. Click on show steps to see.
What is a cross-product?
In the cross-product, two vectors are multiplied. Since vectors have dimensions and magnitudes, they are not multiplied like numerical values.
The famous methods are using the cross-product formula or the cofactor expansion using Sarrus’s rule.
The written form of the vector product is a x b, which is read as a cross b. When two vectors are multiplied, the result is always a vector. The application of this product includes torque and magnetic force.
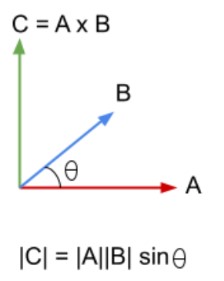
Cross product formula:
The formula used to find cross-product uses the sine function of trigonometry. It is
A x B = |A||B| Sin(θ)
Here;
- |A| is the magnitude of vector A.
- |B| is the magnitude of vector B.
- θ is the angle between A and B.
How to calculate the vector cross product?
Use the 2x2 cross product calculator to find the result. Otherwise, there are two options to find the magnitude of the vector product manually.
Calculating magnitude:
- Apply the aforementioned formula. It works well if the magnitudes and angles are given.
- Use the matrix method. Write the 3-d vectors in a 3 by 3 matrix. Like this:
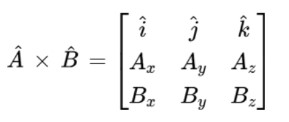
Expand the cofactors to find the formal determinants and simplify.
Since a vector must have some direction, it is necessary to determine it along with the magnitude.
Fun fact: The magnitude of the resultant vector is the same as the area of the parallelogram drawn using the vectors.
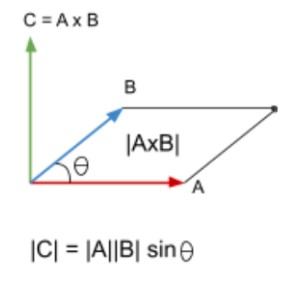
Finding the direction:
The resultant vector of the cross product tells the difference in directions between the original vectors. It is present in the perpendicular axis of both A and B.
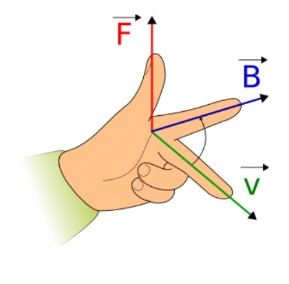
The right-hand thumb rule is very efficient in determining the direction. This rule states that:
“Open your right hand in a way that your forefinger points in the direction of vector A. Point the third or middle finger in the direction of the B vector. The straight thumb indicates the direction of the resultant vector.”
Example:
Find the cross-product of the following vectors.
2 i - 7 j + 2 k
5 i + j - k
Solution:
Step 1: Name the vectors.
A = 2 i - 7 j + 2 k
B = 5 i + j - k
Step 2: Make a 3 by 3 matrix using these vectors.
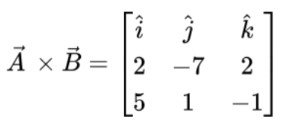
Step 3: Expand using cofactors.
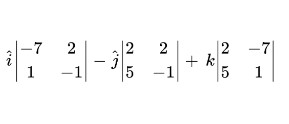
Step 4: Find the determinants and solve them.
A x B = [ (-7).(-1) - (2).(1) ] i - [ (2).(-1) - (2).(5) ] j + [(2).(1) - (-7).(5)] k
= [ (7) - (2)] i - [(-2) - (10)] j + [(2) - (-35)] k
= [ 5 ] i - [ -12 ] j + [ 37 ] k= 5 i + 12 j + 37 k

