To calculate result you have to disable your ad blocker first.
Euler's Method Calculator
Enter the function, put the required points, hit calculate button to find approximated values using Euler method calculator
Euler Method Calculator
Euler Method Calculator is a tool that is used to evaluate the solution of different functions or equations using the Euler method.
What is meant by an Euler method?
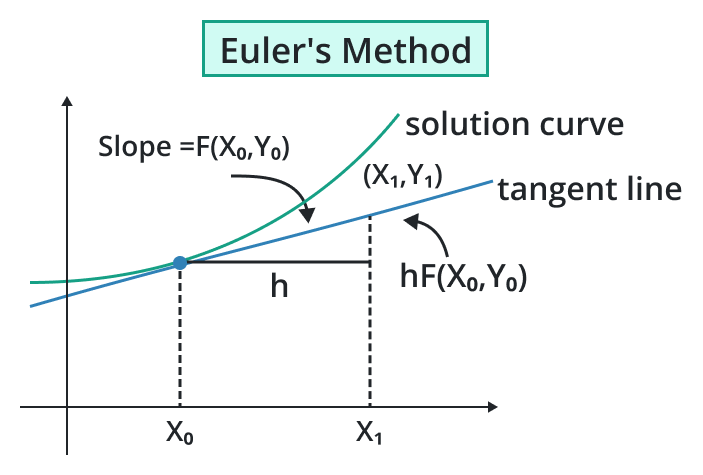
The Euler Method is a numerical technique used to approximate the solutions of different equations. In the 18th century Swiss mathematician Euler introduced this method due to this given the named Euler Method. The Euler Method is particularly useful when there is no analytical solution available for a given equation.
It is a basic numerical method and may not always provide the most accurate results, particularly for complex problems or greater functions with dependence on initial conditions.
Initial Condition:
Put the value of the initial point to start the iterative method and change the value of the point to continue the iteration at the selecting steps. The initial point value is shown as the (t0, y0) where “y0” is the value of the dependent variable of “y” at a given initial point “t0”.
Step Size:
For the easiness of a difficult problem choose a small step size (h) that determines the intervals at which approximate the value of the solution. The smaller the step size increases the accuracy rate and also increases the computation time.
Euler's method Formula
The mathematical formula of the iterative Euler method is stated below.
yn+1 = yn+ h × f(tn,yn)
Where,
- yn+1 = next iterative number
- yn = initial iteration number
- h = step size of the interval
- f(tn,yn) = Value of the function putting its initial values
How to solve problems with the Euler method?
Example 1:
Find the value of the given function if “f(t,y) = t + 4y −3” using the Euler method while the data are given below.
h=4.0, t0=3.0, y0=5.0.
Solution:
Step 1: Write the data.
h=4.0, t0=3.0, y0=5.0
f(t,y)= t + 4y −3
Step 2: Write the general formula of the Euler method.
yn+1 = yn+ h × f(tn,yn)
Step 3: Put the all above values in the above formula and simplify.
h=4.0, t0=3.0, y0=5.0
First start the iteration and put the “n=0” in the general formula it becomes.
y0+1 = y0 + h × f(t0,y0)
y1 = y0 + h × f(t0,y0)
y1=5.0 + 4.0 × 20.0
y1= 85.0
Example 2:
Find the value of the given function if “f(t,y)= t + 4y” using the Euler method while the data are given below.
h=2.0, t0=3.0, y0=4.0.
Solution:
Step 1: Write the data.
h=2.0, t0=3.0, y0=4.0
f(t,y)= t + 4y
Step 2: Write the general formula of the Euler method.
yn+1 = yn+ h × f(tn,yn)
Step 3: Put the all above values in the above formula and simplify.
h=2.0, t0=3.0, y0=4.0
First start the iteration and put the “n=0” in the general formula it becomes.
y0+1 = y0 + h × f(t0,y0)
y1 = y0 + h × f(t0,y0)
y1= 4.0 + 2.0 × 19.0
y1= 4.0 + 2.0 × 19.0
y1= 42.0
Step 4: To find the next iteration find the values of t1.
t1 = t0 + h
t1 = 3.0 + 2.0
t1 = 5.0
f(t1,y1) = t1 + 4y1
f(5,42) = 5.0 + (4)(42.0)
f(5,42) = 5.0 + 168.0
f(5,42) = 173.0
For the second iteration put the “n=1” in the general formula it becomes and put the all above values.
t1 = 5.0, y1= 42.0, f(t1,y1)=173.0
y1+1 = y1 + h × f(t1,y1)
y2 = y1 + h × f(t1,y1)
y2 = 42.0 + 2.0×173.0
y2 = 388.0

