To calculate result you have to disable your ad blocker first.
Equation Solver
Enter the equation and hit calculate button to solve the equation using equation solver
Equation Solver
Equation Solver is a tool used to solve polynomial equations of any order, such as linear or quadratic equations. It employs methods like adding or subtracting the same variable term and manipulating the equation to find the value(s) of the variable that satisfies the equation.
What is meant by equation and expression?
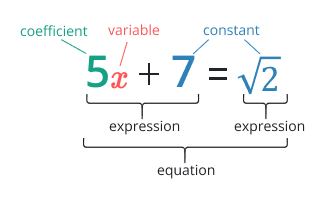
Equation
It states that the two expressions are equal is known as an equation. Simply say that it is a combination of two expressions that are distributive by the equal sign. Equations are useful for clarifying the connection between various variables and a constant. It plays a crucial role in solving many mathematical expressions and problems.
i.e., 2x + 5 = 10 + x is an equation with the variable “x”.
Expression
It is a mixture of numbers, variables, and mathematical operations (such as addition and subtraction) while not an equal sign. Expressions can be as simple as a single number or variable or more complex, involving multiple terms and operations.
i.e., 3x + 7 is the expression with the variable “x”.
How to solve the equation?
Example 1:
4x2 + 2x2 - 4 = 0 solve the equation.
Solution
Step 1: Collect and add the like terms.
(4x2 + 2x2) - 4 = 0
Step 2: Add the polynomial terms together.
(6x2) - 4 = 0
Step 3: Add the constant term from both sides.
6x2 - 4 + 4 = 0 + 4
Step 4: Simplify the left and right-hand side.
6x2 = 4
Step 5: To find the value of “x” divide by “6” on both sides and take square root.
6x2 /6 = 4/6
x2 = 2/3
√x2 = √2/3
x = ∓ 0.8165
Example 2:
4x ^ 2 - 5x - 12 = 0 solve the equation.
Solution
Step 1: Take the given equation and write quadratic formula terms to solve it.
4x ^ 2 - 5x - 12 = 0
a = 4
b = -5
c = -12
Step 2: Now take the quadratic formula.
x = [-b ± √(b2 - 4ac)]/2a
Step 3: Place the value to solve the equation for "x"
x = [-(-5) ± √(-5)2 - 4(4)(-12)]/2(4)
Step 4: Simplify the above equation to find the sum and difference separately.
x = [-(-5) ± √(-5)2 - 4(4)(-12)]/2(4)
x = [5 ± √(25 + 192)]/8
x = [5 ± √217]/8
x = [5 ± 14.73]/8
For Addition
x = [5 + 14.73]/8
x = 19.73/8
x = 2.4663
For Subtraction
x = [5 - 14.73]/8
x = - 9.73/8
x = -1.2163
Frequently Ask Questions (FAQ’s)
How to simplify expression/order equations?
To solve expression/order equations:
First simplify the terms inside parentheses, brackets, braces, and fractions bars.
Evaluate all powers.
Solve all multiplications or divisions from left to right.
Do all additions and subtractions from left to right.
What is the golden rule for solving equations?
The golden rule of algebra is taking a balanced scale. If any operation you apply on one side of the equal sign then you must do the same thing on the other side. i.e., If you multiply by “-2” on the left side then must multiply by “-2” on the other side.
How to solve the linear equation?
To solve the linear equation, get all variables on one side & constant terms on the other side of the equal sign and simplify the terms using algebraic rules such as addition or subtraction.
How to solve the quadratic equation?
Identify the coefficients “a, b, and c” from the quadratic equation “ax2 + bx + c” then Substitute the values into the quadratic formula and Simplify the operations.
Are linear and quadratic equations same?
No, linear equation has the highest degree is one while the quadratic equation highest degree is two. On the other hand, graphically linear shows a straight line graph, and quadratic produces the parabola graph.

