To calculate result you have to disable your ad blocker first.
Denklem Cözücü
Denklemi girin ve bu hesap makinesini kullanarak denklemi çözmek için hesapla düğmesine basın
Table of Contents:
Denklem Çözücü
Denklem Çözücü, doğrusal veya ikinci dereceden denklemler gibi herhangi bir düzendeki polinom denklemlerini çözmek için kullanılan bir araçtır. Denklemi karşılayan değişkenin değerini/değerlerini bulmak için aynı değişken terimini eklemek veya çıkarmak ve denklemi değiştirmek gibi yöntemler kullanır.
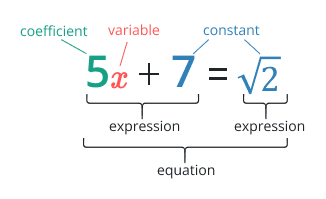
Denklem ve ifade ile ne kastedilmektedir?
Denklem
İki ifadenin eşit olduğunu belirtir. denklem . Basitçe bunun eşit işaretiyle dağılan iki ifadenin birleşimi olduğunu söyleyin. Denklemler, çeşitli değişkenler ile bir sabit arasındaki bağlantıyı açıklığa kavuşturmak için kullanışlıdır. Birçok matematiksel ifadenin ve problemin çözümünde önemli bir rol oynar.
yani, 2x + 5 = 10 + x bir denklem değişkeni ile “ X ”
İfade
Eşittir işareti olmasa da sayıların, değişkenlerin ve matematiksel işlemlerin (toplama ve çıkarma gibi) bir karışımıdır. İfade tek bir sayı veya değişken kadar basit olabileceği gibi birden çok terim ve işlemi içeren daha karmaşık da olabilir.
yani, 3x + 7 bu ifade değişkeni ile “ X ”
Denklem nasıl çözülür?
Örnek 1:
4x 2 + 2x 2 -4 = 0 denklemi çözün.
Çözüm
Aşama 1: Benzer terimleri toplayın ve ekleyin.
(4x 2 + 2x 2 ) - 4 = 0
Adım 2: Polinom terimlerini birbirine ekleyin.
(6x 2 ) - 4 = 0
Aşama 3: Her iki taraftan sabit terimi ekleyin.
6x 2 - 4 + 4 = 0 + 4
4. Adım: Sol ve sağ tarafı basitleştirin.
6x 2 = 4
Adım 5: “ X ” &ldquo'ya böl; 6 ” her iki tarafta ve al kare kök .
6x 2 /6 = 4/6
X 2 = 2/3
&radik; X 2 = &radik; 2/3
x = ∓ 0,8165
Örnek 2:
4x ^ 2 - 5x - 12 = 0 denklemi çözün.
Çözüm
Aşama 1: Verilen denklemi alın ve çözmek için ikinci dereceden formül terimlerini yazın .
4x ^ 2 - 5x - 12 = 0
bir = 4
b = -5
c = -12
Adım 2: Şimdi ikinci dereceden formülü alın.
x = [-b ± &radik;(b 2 - 4ac)]/2a
Aşama 3: "x" denklemini çözecek değeri yerleştirin
x = [-(-5) ± &radik;(-5) 2 - 4(4)(-12)]/2(4)
Adım 4: Toplamı ve farkı ayrı ayrı bulmak için yukarıdaki denklemi basitleştirin.
x = [-(-5) ± &radik;(-5) 2 - 4(4)(-12)]/2(4)
x = [5 ± &radik;(25 + 192)]/8
x = [5 ± √217]/8
x = [5 ± 14.73]/8
İlave için
x = [5 + 14,73]/8
x = 19,73/8
x = 2,4663
Çıkarma için
x = [5 - 14,73]/8
x = - 9,73/8
x = -1,2163

