Algebraic Equations: Definition, Types, applications, and Examples

Algebraic equations have a very vast history. Muhammad ibn Musa al-Khwarizmi was a smart person who lived long ago, in the 9th century. He had a great knowledge of math and stars. That’s the reason, he is known as a mathematician and astronomer.

He is also known as the "father of algebra" because he wrote a book called Kitab al-Jabr that helped people solve math problems in a new way. The word "algebra" actually comes from the name of his book.

Definition of the Algebraic Equation

For a better understanding of algebraic equations. Firstly, we have to understand the concept of algebra. Algebra is a way or a technique of representing equations by using symbols and letters.

An algebraic equation can be defined as a statement in which we use variables, constants, and coefficients with different mathematical operations.

Forms of Algebraic Equation

There are several forms of algebraic equations. A few of them are as follows:

• Linear equations

A linear equation is one in which the highest degree of variable is ‘1’

• Quadratic equations

A type of equation in which the highest degree of the variable is ‘2’ is known as a quadratic equation. It is also known as the 2nd-degree equation.

• Cubic equations

The equation in which the highest degree of the variable is ‘3’ is known as a cubic equation.

• Polynomial equations

These are the equations in which a variable has one or more exponents.

• Radical equations

The equation in which variables come inside the square root.

• Rational equations

The equations in which variables appear as the denominator is known as rational equation.

• Exponential equations

The equation in which variables appear as an exponent is known as the exponential equation.

To solve an equation, it is important to follow the rules and procedures that apply to that specific type of equation. Different types of equations may require different methods to solve, and it is important to choose the appropriate method for each equation to get an accurate solution.

Representation of Equations with their Graphs

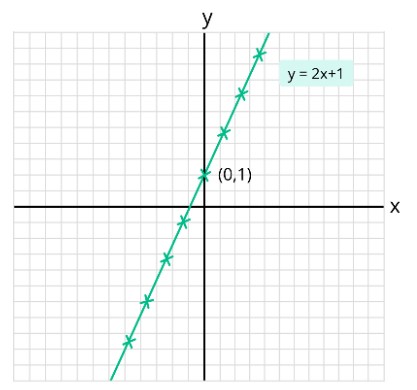
Linear equation

Mathematically,

ax + b = 0

Here,

• ‘a’ is a coefficient of ‘x’ which would always an integer value
• ‘b’ is a constant
• ‘x’ is a variable

linear equation graphical representation

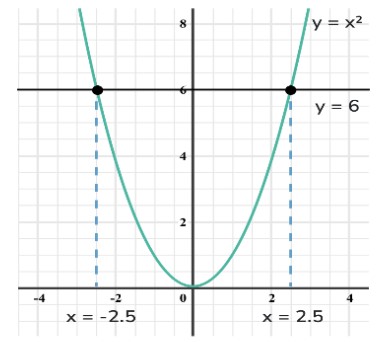
Quadratic equation

Mathematically,

ax^2 + bx +c =0

Here,

• ‘a’ is a coefficient of ‘x^2’ which would always be an integer value
• ‘b’ is a coefficient of ‘x’ which would always be an integer value
• ‘c’ is a constant
• ‘x’ is a variable used in this equation

Graphical representation of quadratic equation

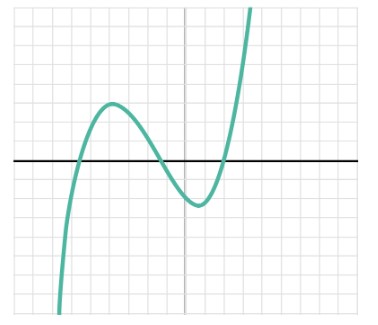
Cubic equation

Mathematically,

ax^3 + bx^2 + cx + d =0

Here,

• ‘a’ is a coefficient of ‘x^3’ which would always be an integer value
• ‘b’ is a coefficient of ‘x^2’ which would always be an integer value
• ‘c’ is a coefficient of ‘x’ which would always be an integer value
• ‘d’ is a constant
• ‘x’ is a variable used in this equation

Graphical representation of Cubic equation

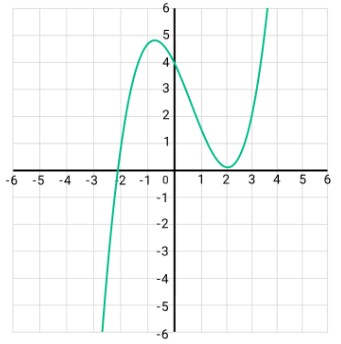
Polynomial equation:

Mathematically,

ax^4 + bx^2 -1 = 0

Here,

• ‘a’ is a coefficient of ‘x^4’ which would always be an integer value
• ‘b’ is a coefficient of ‘x^2’ which would always be an integer value
• ‘-1’ is a constant

Graphical representation of polynomial equation

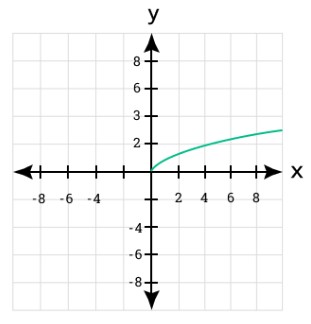
Radical equation

Mathematically,

Sqrt(x+2) + 3 = 5

Here,

• ‘x’ is a variable used in this equation

Graphical representation of radical equation

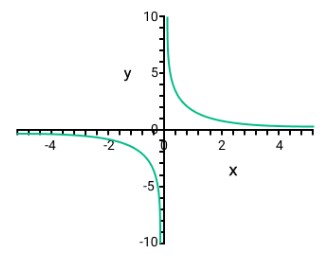
Rational equation

Mathematically,

 (ax + b) / (cx + d) = 1

Here,

• (ax + b) represents the nominator’s equation
• (cx + d) represents the denominator equation
• ‘x’ is a variable used in this equation

Graphical representation of rational equation

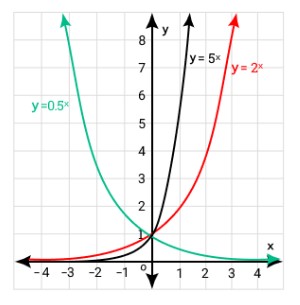
Exponential equation

The equation in which variables appear as an exponent is known as the exponential equation.

Mathematically,

a^x + b = 0

Here,

• ‘x’ is a variable used in this equation as a power of ‘a’
• ‘b’ is a constant

Graphical representation of exponential equation

Applications of an algebraic equation

Some applications are as follows:

• Solving for unknown values
• Modeling real-world phenomena
• Analyzing data
• Optimizing solution
• Designing experiments

Examples

Examples of algebraic equations are as follows:

Example 1:

Find the value of the ‘x’ if (2x + 4) = 0.

Solution:

Step 1: write the equation

2x + 4 = 0

Step 2: subtract the ‘4’ on both sides of the equation

2x + 4 – 4 = 0 – 4

2x = - 4

Step 3: Using the property of algebra

x = -4 / 2

x = -2

Example 2:

Find the value of “x” when (x^2 + 7x + 10) = 0.

Solution:

Step 1: Write the equation

x^2 + 7x + 10 = 0

Step 2: Make polynomial factors of the given equation

x^2 + 5x + 2x + 10 = 0

x (x + 5) + 2 (x + 5) = 0

(x + 2) * (x + 5) = 0

Step 3: Find the value of “x” by using the algebraic properties

x = -2, -5

Summary

This article explains algebraic equations, including their concepts, rules, formulas, and applications. It also uses practical examples and scenarios to help you understand the concept of algebraic equations and apply them easily.