To calculate result you have to disable your ad blocker first.
Polynomial Factoring Calculator
To use polynomial factoring calculator, input the polynomial function and hit the calculate button
Polynomial Factoring Calculator
Polynomial factoring calculator is used to make the factors of the given polynomial function.
What is Polynomial Factoring?
Polynomial factoring is the process of finding the factors of a polynomial expression. It involves expressing a polynomial as a product. The goal is to find the roots (zeros) of the polynomial and express the polynomial in terms of its factors, which can be useful in solving equations, graphing polynomials, and simplifying expressions.
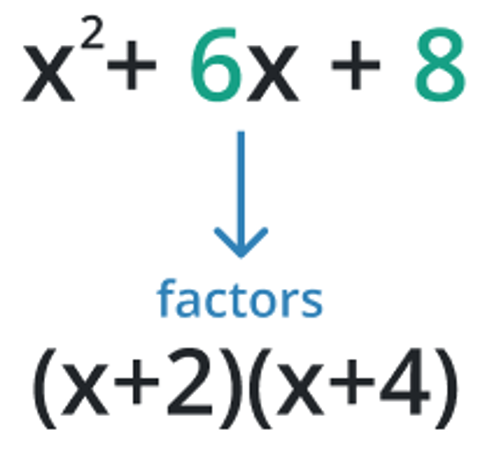
Methods of Finding Polynomial Factoring
To find the factoring of polynomials there is no general way to find them, but we have some methods based on formulas, the degree of polynomials, and a number of terms.
Grouping
This method involves grouping terms of the polynomial and using common factors to simplify. For example, consider the polynomial x2 + 6x + 9. We can group the first two terms, (x2 + 6x), and the last two terms, (6x + 9), and factor a common factor of 3 from each group, giving us (3x + 3) (x + 3).
Factoring by grouping
This method involves grouping terms of the polynomial and then factoring by finding a common factor. For example, consider the polynomial x3 + x2 + x. We can group the first two terms, (x3 + x2), and the last two terms, (x2 + x), and factor a common factor of x from each group, giving us x (x2 +1).
Factoring by inspection
Looking at the polynomial and finding a pattern that can be factored in. For example, consider the polynomial x2 + 4x + 4. We can see that the last term, 4, is twice the middle term, 2x, so we can factor a common factor of 2 from the middle term, giving us (x + 2) (x + 2).
Factoring by using special formulas
The method involves using special formulas to factor in specific types of polynomials. For example, consider the polynomial x2 - z2. We can factor this using the difference of squares formula, which states that a2-b2= (a+b) (a-b), giving us x2 - z2 = (x + z) (x - z).
How to calculate quartiles of a data set?
In the below examples, the method of finding factors is explained briefly.
Example 1
Find the factors of the polynomial 2x3+4x2+2x.
Solution
Step 1: First we have to take the common from the expression.
2x(x2+2x+1)
Step 2: Now we have to make the factor in such a way when we multiply we get 1x^2 and when we add them we get 2x.
2x(x2+ x + x + 1)
Step 3: Now we take the common from 1st two terms and the last two terms such that
2x(x(x+1) + 1(x+1))
Step 4: So take the common from the expression we have:
2x(x+1) (x+1)
Example 2:
Find the factors of the polynomial x4-1.
Solution:
Step 1: The expression involves two square terms with a minus sign. We have to apply the a2-b2 formula:
a2-b2= (a+b) (a-b)
(x2)2 – (1)2=(x2-1)(x+1)
Step 2: We have again a term to which we can apply the formula
(x2-1) (x2+1) =(x+1) (x-1) (x2+1)
x4-1 =(x+1) (x-1) (x2+1)

