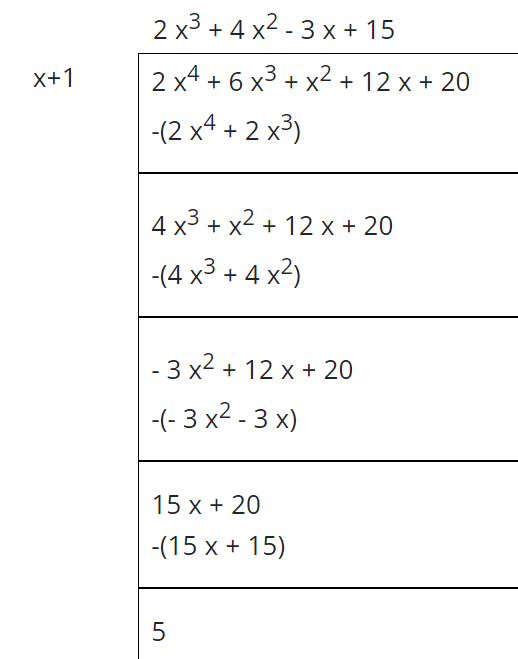Polynomial Long Division Calculator

Polynomial Long Division Calculator

Polynomial long division calculator is used to divide the polynomial functions by taking the divisor and dividend. This divide polynomials calculator finds the quotient and remainder of the given functions. 

What is polynomial long division?

Polynomial long division is a method used to perform polynomial division. In this method of polynomial division, the higher degree polynomial is the dividend and the lower degree polynomial is the divisor.

How to solve the problems of polynomial long division?

The problems of polynomial long division can be solved easily either by using a calculator or manually. Let’s take an example to understand this concept.

Example

Find the polynomial long division if the dividend of the polynomial is 2x⁴ + 6x³ + x² + 12x + 20 and the divisor is x+1.

Solution 

Step 1: Divide the leading term of the dividend of the polynomial by the leading term of the divisor to get the first term of the quotient. 

2x4/x = 2x3

This means you have to multiply the divisor by 2x³ to get the first step.

2x3(x+1) = 2x4+2x3

The remainder must be 4x³ + x² + 12x + 20

Step 2: Now again divide the leading term of the remainder of the polynomial by the leading term of the divisor.

4x3/x = 4x2

Multiply the divisor by 4x² to get the second step.

4x2(x+1) = 4x3+4x2

The remainder must be -3x² + 12x + 20

Step 3: Repeat the above steps again to get the third remainder of the division.

-3x2/x = -3x

Multiply the divisor by -3x to get the third step.

-3x(x+1) = -3x2-3x

The remainder must be 15x + 20

Step 4: Now divide the leading term of the above remainder by the first term of the divisor. 

15x/x = 15

Multiply the divisor by 15 to get the third step.

15(x+1) = 15x + 15

The remainder must be 5.

This is the final step as there is no variable left in the remainder of the division. 

Hence 

Quotient = 2x³ + 4x² – 3x + 15

Remainder = 5

Step 5: Mathematically the polynomial long division is: