Synthetic Division Calculator

Synthetic Division Calculator

Synthetic division calculator is a tool that performs synthetic division by using the polynomial as a numerator and linear factor as a denominator. The synthetic division calculator gives a step-by-step solution to every problem.

Definition of Synthetic division

Synthetic division is a method of dividing polynomials by linear factors. It is a very simple technique to divide the polynomial with the linear factor of the form “x-c”. Where “c” is a self-determined constant.

Formula

The formula of synthetic division is stated as follows.

P(x)/(x-c) = Q(x) + R/(x-c)

Where,

• P(x) = dividend polynomial of any order.
• (x-c) = linear factor of degree 1.
• Q(x) = quotient polynomial formed after applying the synthetic technique.
• R = constant quantity known as the residual or remainder.

Example of Synthetic Division

Solve the question by synthetic division if,

Numerator polynomial = 7x⁴+2x²-2

Denominator polynomial = x-2

Solution:

Step 1: Write the given data.

P(x) = 7x⁴+2x²-2

Linear factor = x-2

P(x)/Linear factor = (7x⁴+2x²-2)/ (x-2)

Step 2: write the coefficients of the numerator polynomial and write them from greatest to least.

7, 0, 2, 0, −2

Step 3: put the denominator term equal to zero and find the value of the unknown variable.

x−2=0

x=2

Step 4: write the above data in the synthetic division and simplify.

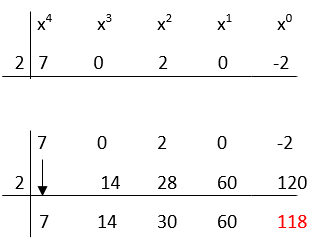
The quotient is 7x³ + 14x² + 30x + 60 and the remainder is 118.

Step 5: write the value according to the synthetic division formula.

Q(x) = 7x³ + 14x² + 30x + 60, R = 118, and c = 2

[7x⁴+2x²-2/ x-2] = (7x³ + 14x² + 30x + 60) + [118/ (x-2)]

Some other examples

Here are a few results of other examples in the table section.