Fourier Series Calculator

Fourier Series Calculator

Use the Fourier series calculator to represent any periodic function in terms of sin and cos. The Fourier series solver calculates the three unknown coefficients and puts them in the general series. The result is provided after simplification.

What is a Fourier Series?

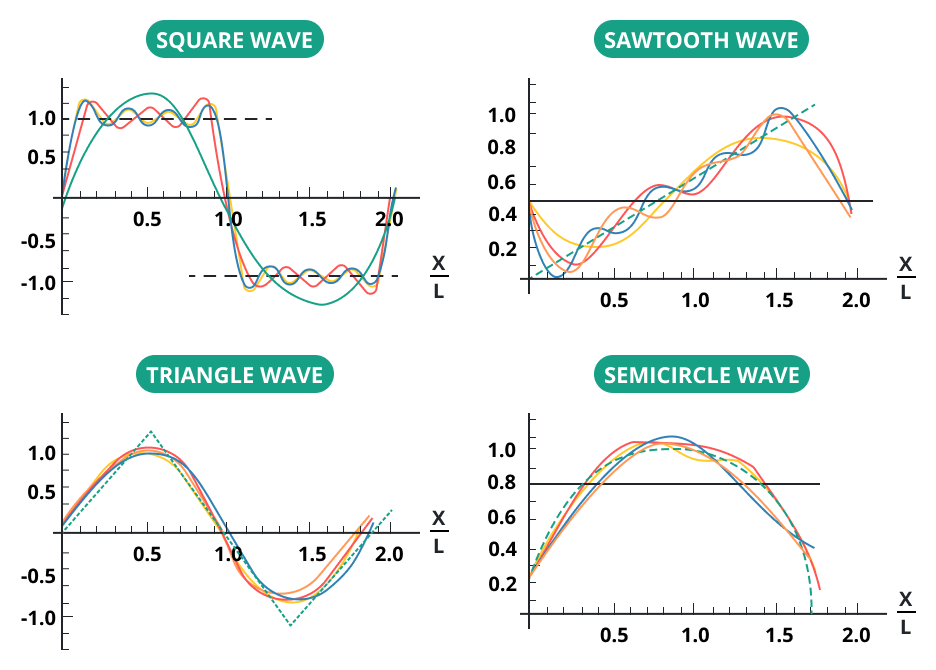
A Fourier series is a way to express a periodic function (a function that repeats its values at regular intervals) as a sum of sine and cosine functions. 

These sine and cosine functions are known as the harmonics of the original function. The more harmonics we include, the more accurately we can represent the original function.

Mathematically, a Fourier series can be written as:

f(x) = a₀ + Σ[a_n cos(nx) + b_n sin(nx) ]

Here,

• f(x) is the periodic function,
• a₀, a_n, and b_n are coefficients 
• n is the order of the Fourier series.

The order determines the number of derivatives (maximum 5) used in the representation.

Fourier series formula:

The coefficients  a₀, a_n, and b_n are calculated using the following formulas.

a₀ = (1/L) ∫[ f(x) dx ] over the interval [-L/2, L/2]

a_n = (1/L) ∫[ f(x) cos((2πn x)/L) dx ] over the interval [-L/2, L/2]

b_n = (1/L) ∫[ f(x) sin((2πn x)/L) dx ] over the interval [-L/2, L/2]

Here, L is the period of the function f(x). These formulas assume that the function has a period of L and is symmetric around the origin. In the case of a non-symmetric function, you may need to adjust the intervals for the integral calculations.

How to calculate the Fourier series?

Example:

f(x) = 1 if 0 < x < π and f(x) = -1 if π < x < 2π.

The Fourier series representation of this function will be in the following form:

f(x) = a₀ + Σ[a_n cos(nx) + b_n sin(nx) ]

To calculate the coefficients a₀, aₙ, and bₙ, we need to use the following formulas:

a₀ = (1/π) ∫[ f(x) dx ] over the interval [0, 2π]

a_n = (1/π) ∫[ f(x) cos(nx) dx ] over the interval [0, 2π]

b_n = (1/π) ∫[ f(x) sin(nx) dx ] over the interval [0, 2π]

• First, let's calculate a₀:

a₀ = (1/π) ∫[ f(x) dx ] = (1/π) [ ∫(1 dx) from 0 to π + ∫(-1 dx) from π to 2π ]

a₀ = (1/π) [ (x)|₀^π - (x)|π^(2π) ] = (1/π) [π - 0 - (2π - π)] = 0

• Now, let's calculate a_n

a_n = (1/π) ∫[ f(x) cos(nx) dx ] = (1/π) [ ∫(cos(nx) dx) from 0 to π + ∫(-cos(nx) dx) from π to 2π ]

a_n = (1/π) [ (sin(nx)/n)|₀^π - (sin(nx)/n)|π^(2π) ]

Since sin(nπ) = 0 for all integer values of n, we get:

a_n = 0 for all n.

• Finally, let's calculate b_n:

b_n = (1/π) ∫[ f(x) sin(nx) dx ] = (1/π) [ ∫(sin(nx) dx) from 0 to π + ∫(-sin(nx) dx) from π to 2π ]

b_n = (1/π) [ (-cos(nx)/n)|₀^π + (cos(nx)/n)|π^(2π) ]

b_n= (1/π) [ (-cos(nπ)/n + 1/n) + (cos(2nπ)/n + cos(nπ)/n) ]

For even values of n, cos(nπ) = 1, and for odd values of n, cos(nπ) = -1. Therefore, bₙ = 0 for even n, and for odd n:

b_n = (1/π) [ (-(-1)/n + 1/n) + (1/n + 1/n) ] = (1/π) [ 2/n + 2/n ] = (4/π) [ 1/n ]

Now we have all the coefficients, and the Fourier series representation of the given square wave function is:

f(x) = Σ[ (4/π)(1/n) sin(nx) ] for odd n.

Applications of Fourier Series

Fourier series have a wide range of applications, including:

Signal Processing: Fourier series are used to analyze and process signals in fields such as telecommunications, audio engineering, and image processing.

Vibration Analysis: Engineers use the Fourier series to understand the behavior of vibrating systems and design better mechanical structures and machines.

Heat Transfer: In thermodynamics, the Fourier series is used to analyze heat transfer and diffusion processes.

Electrical Circuits: These series also help in understanding the behavior of electrical circuits and designing efficient power systems.