To calculate result you have to disable your ad blocker first.
Geometric Sequence Calculator
Provide the value of the first term, ratio, and the term you want to find (nth term) to the geometric sequence calculator.
Geometric Sequence Calculator
The geometric progression calculator finds any value in a sequence. It uses the first term and the ratio of the progression to calculate the answer. You can enter any digit e.g 7, 100 e.t.c and it will find that number of value.
This tool gives the answer within a second and you can see all of the steps that are required to solve for the value, yourself.
What is a sequence?
In general, a sequence is a set of integers that go on with a flow. It means that each term is different from its previous value in the same way as the term next to it is from itself. For example:
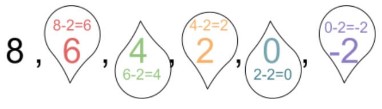
All of the values in this sequence differ from their previous value by -2.
What is a Geometric sequence?
The Definition of a geometric sequence is:
“Such a sequence in which the difference (d) between the two consecutive terms is a ratio (r)”
Each new term is found by multiplying the preceding term with this ratio.
Geometric sequence formula
We use a formula to find any number value in a geometric sequence. This formula is:
an = a1 rn-1
In this equation;
- an is the term we want to find.
- a1 is the first term of the sequence.
- r is the ratio.
- n is the number of the number we need.
How to find the nth value in a geometric sequence?
One way is to use the geometric sequences calculator. The second option is manual. To learn how to find the nth term in a geometric progression, see the example ahead.
Example
Find the 8th term for a sequence. The first value of the sequence is 3. The ratio between the terms is 2/3.
Solution:
Step 1: Identify the values.
a1 = 3
r = 2/3
n = 8th
Step 2: Use the values in the formula.
an = a1rn-1
a8 = (3)(⅔)8-1
a8 = (3)(⅔)7
a8 = (3)(0.000914)
a8 = 0.0027

