To calculate result you have to disable your ad blocker first.
Arithmetic Sequence Calculator
Enter the values in the below input boxes to calculate the nth term and sum of arithmetic progression by using arithmetic sequence/series calculator.
Nth Term Calculator
Arithmetic sequence calculator is an online tool that calculates:
- Arithmetic Sequence
- Nth term value
- Sum of arithmetic sequence
What is an arithmetic sequence?
Arithmetic sequence can be defined as,
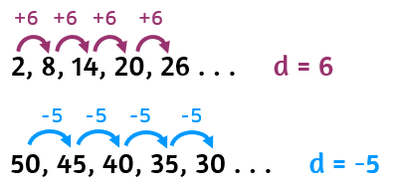
“An arithmetic sequence is a sequence where each term increases by adding or subtracting some constant value known as common difference (d).”
Arithmetic sequence is commonly known as arithmetic series and arithmetic progression as well.
Arithmetic sequence formula
Formula to find the nth term is:
nth term = a + (n - 1)d
Formula to find the sum of an arithmetic progression is:
S = n/2 × [2a₁ + (n - 1)d]
Where:
- a refers to nᵗʰ term of the sequence,
- d refers to the common difference, and
- a₁ refers to the first term of the sequence.
There is no specific formula to find arithmetic sequence. In the next section, we will explain the method to calculate arithmetic sequence using common difference and first term.
Finding the nth term, arithmetic sequence, and its sum
For the calculation of the nth term, arithmetic sequence, and its sum, you can simply use the arithmetic series calculator above.
Example:
Find the nth term and sum of the arithmetic sequence for 15 number of terms if the first term is 5 and the difference is 4.
Solution:
Step 1: Identify the values.
n = 15
a = 5
d = 4
Step 2: Use the arithmetic sequence formula and place the values.
For finding the nth term
nth term = a + (n - 1)d
= 5 + (15 - 1) × 4
= 61
nth term = 61
For finding the sum of an arithmetic sequence
S = n/2 × [2a₁ + (n - 1)d]
S = 15/2 × [2(5) + (15 - 1) × 4]
S = 495
For finding the Arithmetic Sequence
Add a common difference in the first term to get the arithmetic sequence. Keep adding the common difference in the preceding number till you get the last number in the sequence.
| For n = 1 | a1 = 5 |
| For n = 2 | a2 = a1 + d = 5 + 4 = 9 |
| For n = 3 | a3 = a2 + d = 9 + 4 = 13 |
| For n = 4 | a4 = a3 + d = 13 + 4 = 17 |
| For n = 5 | a5 = a4 + d = 17 + 4 = 21 |
| For n = 6 | a6 = a5 + d = 21 + 4 = 25 |
| For n = 7 | a7 = a6 + d = 25 + 4 = 29 |
| For n = 8 | a8 = a7 + d = 29 + 4 = 33 |
| For n = 9 | a9 = a8 + d = 33 + 4 = 37 |
| For n = 10 | a10 = a9 + d = 37 + 4 = 41 |
| For n = 11 | a11 = a10 + d = 41 + 4 = 45 |
| For n = 12 | a12 = a11 + d = 45 + 4 = 49 |
| For n = 13 | a13 = a12 + d = 49 + 4 = 53 |
| For n = 14 | a14 = a13 + d = 53 + 4 = 57 |
| For n = 15 | a15 = a14 + d = 57 + 4 = 61 |
Arithmetic Sequence = 9, 13, 17, 21, 25, 29, 33, 37, 41, 45, 49, 53, 57, 61
Use the arithmetic progression calculator above to verify the value of the nth term and arithmetic sequence.

