To calculate result you have to disable your ad blocker first.
What is an Arc? Explained With Examples
Publish Date: 08 Aug, 2023
Table of Content
The basic component of geometry plays a very important role in understanding the concept of geometrical shapes known as an arc. It is also known as the curve of a circle that plays a key role in different mathematical concepts and also in real-life applications.
In simple words, we can say that an arc is a portion of the circumference of a circle. In a circle, it is made up of two endpoints that are connected through a smooth curve.
What is an Arc?
In mathematics, an arc represents the boundary portion of the circumference of a circle. The term arc is used in the condition of the circle and other curve shapes. An arc is a portion with two endpoints in the circumference of the circle. These points are unique.
The radi of the arc lies between these two endpoints. We can measure the length of an arc by using the angle and the value of radi lies between these endpoints. Also, the nature of an arc depends on the curvature of the shape.
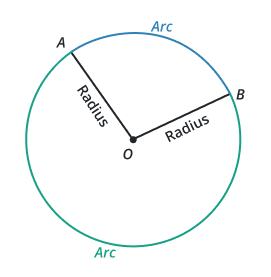
In the above figure, the curve BA represents an arc.
Formulation of an Arc
The formula for finding the length of an arc is as follows:
l = r * θ
Here,
- “l” represents the length of an arc
- “r” represents the radius
- “θ” represents the angle
Types of an Arc
Some types of an arc are as follows:
- Minor arc
- Major arc
- Semi-circular arc
- Equidistant arc
- Overlapping arc
- Intersecting arc
- Tangent arc
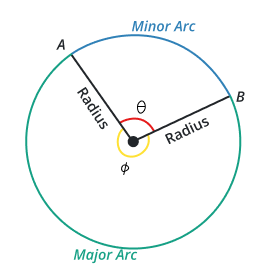
Minor & Major Arc
A minor arc is one that is less than a semicircular arc in size. The length of the minor arc is less than 180o of the circle’s diameter.
A major arc is one that is larger arc than a semicircular arc. The length of the major arc is larger than 180 degrees of the circumference of the circle.
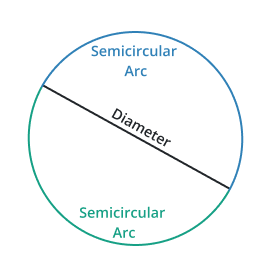
Semi-circular arc
The arc whose length is equal to 180 degrees is known as a semi-circular arc. The length of that arc covers the circumference of a complete semi-circle.
Equidistant arc
An arc that is equally distant from a given point or line is known as an equidistant arc. In an equidistant arc, all the points have the same distance from the given point or line.
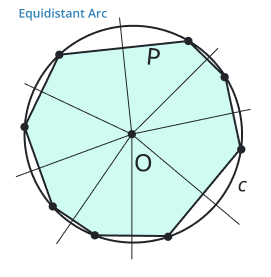
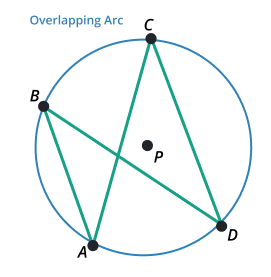
Overlapping arc
The arc in which two arcs share a common portion or section. Those two arcs are also part of the curve. The arc which shares a common potion or section is known as an overlapping arc.
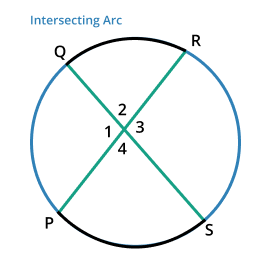
Intersecting arc
The arc shares the same endpoints and at some point within the circle they intersect each other is known as an intersecting arc. The sum of their individual measures is known as the measure of intersecting arcs.
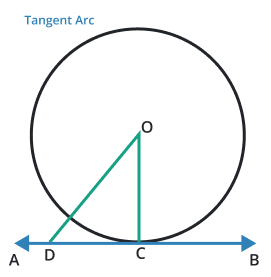
Tangent arc
An arc that is tangent to the point or line at a curve of an arc is known as a tangent arc. In this, it touches on a single point but does not intersect the line or point.
Applications
Some applications of an arc are as follows:
- Geometry
- Architecture and design
- Engineering
- Trigonometry
- Art
- Optics and lens design
- Computer graphics and animation
Geometry
Arc plays an important role in geometry. We can’t understand the basic concept of geometry until we don’t have complete knowledge of an arc.
Architecture and design
The concept of an arc is also used in design and architecture. The dome of the different types of buildings is made by using the concept of the curve which is basically a part of an arc.
Engineering
Engineers used the concept of an arc in structural analysis and design. Arcs are also useful to understand the path of moving objects, like projectiles and vehicles.
Trigonometry
Arc plays a central role in trigonometry. It is used to find the length of an arc of a geometrical shape by using the angle. If we have the value of angle and radius then we can easily find the value of arc length.
Art
The concept of an arc is also used in art. If we have a great knowledge of an arc then we can be a good artist too. Art is not an easy work. Artist all over the world uses different sources to use symbols, generate visual attraction, and raise the flame of emotional response in the audience.
Optics and lens design
Arcs are also used in the designing of optical things, such as lenses and glasses. As we studied, there are two types of lenses. One is convex and the other is concave. The formation of both lenses depends upon the knowledge of an arc.
Computer graphics and animation
In the field of computer graphics and animation arcs also play an important role, graphics designers use them to make their animation or visualization realistic. Also, the movement of their animation also depends on an arc.
Examples
Some examples of finding an arc length are as follows:
Example 1:
Find the arc length if θ = 3.143 radians and r = 6cm.
Solution
Step 1: Assemble the data.
θ = 3.143 radians
r = 6 cm
l =?
Step 2: By using the formula.
l = r * θ
Step 3: By putting the values.
l = 6 * 3.143
l = 18.858 cm
This is the way of finding the value of arc length.
Example 2:
Find the length of an arc if r = 10 cm, θ = 0.5 radians.
Solution
Step 1: Collect the data and rearrange it.
r = 10 cm
θ = 0.5 radians
l =?
Step 2: By using the formula.
l = r * θ
Step 3: Substitute the values.
l = 10 * 0.5
l = 5 cm
wrap up
In the above article, we've discussed the basics of an arc. We described the introduction of an arc, its definition, the formula for finding the arc length, types, applications, and examples. Arc plays a very important role in the everyday activity of life.
Many fields are nearly incomplete without the complete knowledge or basic concept of an arc. After a complete overview, everyone would be able to understand the concept of arc and utilize this knowledge according to his/her needs.

