To calculate result you have to disable your ad blocker first.
Interpolation Calculator
Enter the coordinate point’s value in the respective fields and press the calculate button to interpolate value of given points using our Interpolation Calculator.
Interpolation Calculator is an online tool that helps to calculate the interpolated value for the “y” linear function of the given coordinates values. This linear interpolation tool makes complex calculations faster and shows the interpolated value of given coordinates with detailed steps in fraction seconds.
What is interpolation?
In mathematics, Interpolation is the process of finding the new value of any function by using the already-known values of any data. For this use the specific linear function and determine the value of the unknown variable. According to Wikipedia, linear interpolation can be defined as:
“Linear interpolation is a process of fitting the curve by using the linear polynomial function to construct the new data points by using the known data points.”
For this use the specific formula that is named the linear interpolation formula. The linear interpolation for any Point (X, Y) is graphically represented in the below fig.
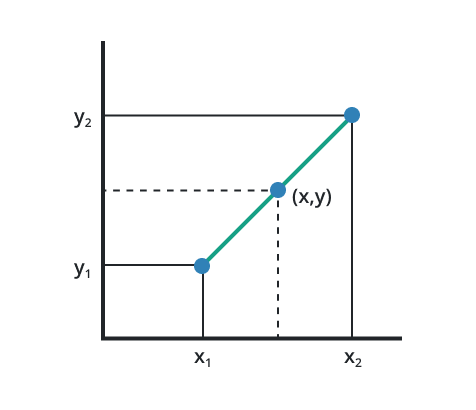
Linear interpolation is specifically used to estimate the unknown coordinate value that falls between the two known values and is also useful in determining the intermediate value of the set of data points. Its application is found in data forecasting, interpolating the predictive results of the stock market, and financial modeling.
Linear Interpolation Formula
The linear interpolation formula is used to interpolate the new value of the given function by using the coordinate value of the two given points. Let the two coordinate points be (X1, Y1) & (X2, Y2). The value of the X-coordinate is also given where the interpolation is done and its formula can be stated as:
Linear Interpolation formula = Y = (X - X1) x (Y2 - Y1)/(X2 - X1) + Y1
Where,
- Y = required interpolated value
- X1 & Y1= x-coordinate & y-coordinate value of first point
- X2 & Y2= x-coordinate & y-coordinate value of the second point
- X = x- coordinate value where interpolation performed
To find the value use our above linear interpolation calculator by entering the values in the given input fields, which performs the calculation without using any specific formula with detailed steps.
How to Perform the Linear Interpolation?
Here solve the examples of linear interpolation equations using the linear Interpolation formula with the detailed steps.
Example:
Evaluate the value of “Y” using the linear interpolation formula at X = 4 and the given set of values are (3, 4) & (6, 8).
Solution:
Step 1: Collect the data from the given statement.
X = 5, X1 = 4, X2 = 6,
Y = ?, Y1 =4, Y2 = 8,
Step 2: Put the values in the linear interpolation formula.
Y = (X - X1) x (Y2 - Y1)/(X2 - X1) + Y1
= (5 - 4) x (8 - 4)/(6 - 4) + 4
Simplify the expression using algebraic rules.
= (1) x (4)/(2) + 4
= (4/2) + 4
= 2 + 4
Y = 6
To, verify the interpolated value using the above online interpolation calculator.
Example:
Evaluate the interpolated value of “Y” at the given set of values are (5, 3.5) & (10, 6) and X= -3.
Solution:
Step 1: Write the values of coordinate from the given conditions.
X = -3, X1 = 5, X2 = 7.5,
Y = ?, Y1 = 3.5, Y2 = 6,
Step 2: substitute all values in the linear interpolation formula.
Y = (X - X1) x (Y2 - Y1)/(X2 - X1) + Y1
= (-3 - 5) x (6 – 3.5)/(7.5 - 4) + 3.5
Simplify the expression using algebraic rules.
= (-8) x (2.5)/(2.5) + 3.5
= (-20/2.5) + 3.5
= -8 + 3.5
Y = -4.5
Similarly, you can use our above interpolation calculator to perform the linear interpolation for any coordinates.
Frequently Asked Questions
What is the use of the Linear Interpolation formula?
Linear interpolation formula is a technique that is useful for curve fitting by finding the unknown values by using the known set of data with the help of a linear polynomial function. Moreover, it is also used in data prediction, market research, data forecasting, and many others.
How to perform the interpolation on a set of values?
Note all data values carefully and put all data values in the linear interpolation formula then simplify to get the required interpolate value. To match the results use our linear interpolation calculator, by putting the values in the given inputs.
How do you interpolate value with an online interpolation calculator?
Put all coordinates values in the respective input fields according to the data points and press the “calculate” button or get the final result with the detailed steps.
Why interpolation is called linear interpolation?
In the process of finding the interpolated value use the linear polynomial function with degree 1. Thus, due to the use of linear function, the interpolation is also called linear interpolation

