Interval Notation Calculator

Interval Calculator 

Interval calculator is used to calculate the number line of open and close intervals based on the inequality of the numbers. This interval notation calculator solves the open, semi-open, semi-close, and close intervals in a fraction of a second.

What is the Interval?

A mathematical interval is a group of real numbers that fall between two given values known as the interval's endpoints. The set comprises all of the numbers that fall between the set's two ends.

They may or may not be included in the set, depending on the interval's "type" or notation.

Types of interval notation

Here are the types of intervals:

1. Open interval

In open intervals, the endpoints are not included.  Let us have an open interval a to b which is represented by (a, b) between round brackets. If a number k lies between a b interval it is represented as a < k < b.

2. Closed interval

A closed interval is defined as all the points and boundary points included in it. Let us have an interval a to b which is represented as [a, b] between two square brackets. If a number k lies between them, it will be represented as a ≤ k ≤ b.

3. Right open and left closed interval

A right open means that the right boundary is not included and a left closed means that the left boundary is included. If we have an interval a to b then it is represented by (a, b]. If a number k lies between them it will be represented as a < k ≤ b.

4. Left open and right closed interval

A left open means that the left boundary is not included and a right closed means that the right boundary is included. If we have an interval a to b then it is represented by [a, b). If a number k lies between them it will be represented as a ≤ k < b.

How to find the length of the interval?

Interval length can be defined as the difference between their boundaries.

Let [a, b] be an interval so the length is defined as

Length of the interval = b-a

Examples of interval notation

We will discuss some examples of intervals with the help of number lines and inequalities.

Example 1: For semi-close interval

Plot the interval [2,9) on the number line and also write the inequality and length of the interval.

Solution:

Step 1: First we make an Inequality.

The interval is right close and left open so it means the right boundary is included and the left is excluded.

2≤x<9

Step 2: Now the number line is

 
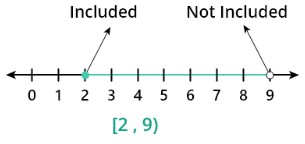
Step 3: The length of the interval is 

9-2 = 7

Example 2: For open interval

Plot the interval (-9, -5) on the number line and also write the inequality and length of the interval.

Solution:

Step 1:  The Inequality of the interval (-9, -5) both the boundary of the interval is excluded so

-9<x<-5<x<-5< p=> </x<-5<x<-5<>

Step 2: The number line is 

 
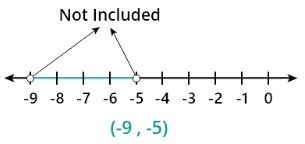
Step 3: The length of the interval is

-5-(-9) = 4

Example 3: For semi-close interval

Plot the interval (-2,3] on the number line and also write the inequality and length of the interval.

Solution:

Step 1: The Inequality of the given interval is

-2<x≤3< p=> </x≤3<>

Step 2: Number line 

 
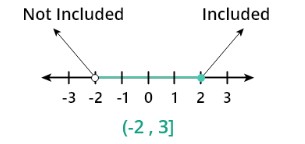
Step 3: Length of the interval 

3-(-2) = 5

Example 4: For close interval

Plot the interval [-5,2] on the number line and length of the interval, and write the inequality.

Solution:

Step 1:  The Inequality of the interval [-5,2] Both the boundaries of the interval are included so  

-5 ≤ x ≤ 2

Step 2: Number line

 
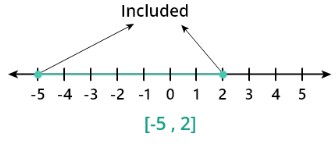
Step 3: Length of the interval 

2-(-5) = 7

References

• What is the interval? Study.com | Take Online Courses. Earn College Credit. Research Schools, Degrees & Careers. (n.d.)
• Types of Interval notation. Brilliant Math & Science Wiki. (n.d.).