Newton's Method Calculator

Newton's Method Calculator

Newton's Method Calculator is used to evaluate the value of an independent variable that makes the function equal to zero. It is usually used to find the roots of a function. The derivative of the function will be taken in this iterative method to improve the estimated roots of the function after each iteration. 

This Newton's Method Calculator is a powerful tool to solve complex functions that are difficult to solve manually. 

What is Newton’s Method?

Newton’s method is used to find the approximate solution of a polynomial by using the irritation method. This method is an iterative method that repeats a number of steps for the solution which is very close to the exact solution of the function. We have to decide on an initial value by guessing which is close to the answer to a rapid result.

Formula:

Let a function f(x), then the general formula is given below

$$f\left(x_{n+1}\right)\:=x_n-\:\frac{f\left(x_n\right)}{f'\left(x_n\right)}$$

• n = 0,1,2, 3, ...
• xn is the initial value.
• f(xn) is the initial value of the function
• f′(xn) is the 1st derivative at xn.

Why do we use Newton’s Method?

For the linear equation ax+b=0 we find the solution of x = -b/a, similarly, for the quadratic equation we have to build a formula to calculate the roots of the given polynomial. We have some other methods to get the roots until degree four.

But if the degree of the polynomial is five or greater than five we have no exact formula of find the solution. So we use a numerical approach to get the solution of the polynomial. This approach is known as Newton’s method.

Graphically interpretation:

Let a function f(x), estimate the value of the function at x₀. We draw a tangent line to f at x₀. If the derivative of a function at x₀ is not equal to zero, then the line intersects on the x-axis at some point (x1,0). 

Now let x₁ be the next point for approximation to the actual root. The x₁ is closer than x₀. Now draw the next tangent line at a point x₁. If the derivative at the point x₁ is not equal to zero. Then the line also intersects the x-axis at some point. Continue the procedure until we get to close the actual root.

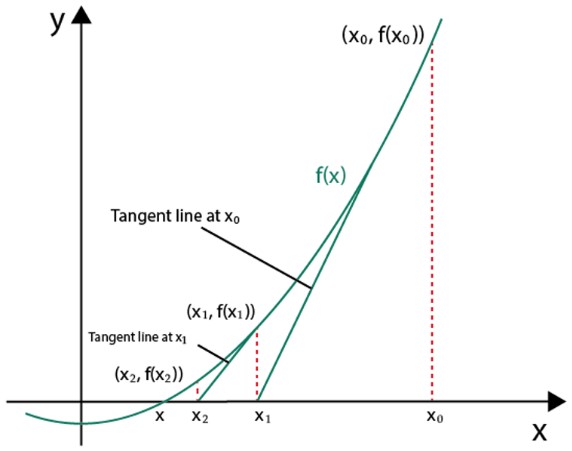
Example of Newton's Method

To understand the method, we discuss an example with step by step solution.

Example 

If we have a function 3x^2+sin(x). find the solution using Newton’s Method where the starting point is 2 and the number of iterations is 3.

Solution:

Step 1: The general formula 

$$f\left(x_{n+1}\right)\:=x_n-\:\frac{f\left(x_n\right)}{f\:'\left(x_n\right)}$$

Step 2: Take the given function and its derivative.

f(x)= 3x² + sin(x)

f′(x)= 6x + cos(x)

Step 2: Now put n = 0 at x₀ = 2

f(x₀) = 3x² + sin(x) = 3(2)² + sin(2) 

f(x₀) = 12.91

f′(x₀) = 6x+cos(x) = 6(2)+cos(2)

f′(x₀) =11.58

$$f\left(x_1\right)\:=x_0-\:\frac{f\left(x_0\right)}{f'\left(x_0\right)}$$

$$f\left(x_1\right)=2-\frac{12.91}{11.58}$$

f(x₁) = 0.89

Step 3: Now put n = 1 at x₁ = 0.89

f(x₁) = 3x² + sin(x) = 3(0.89)² + sin(0.89) 

f(x₁) = 3.13

f′(x₁) = 6x+cos(x) = 6(0.89)+cos(0.89)

f′(x₁) =5.95

$$f\left(x2\right)\:=x_1-\:\frac{f\left(x_1\right)}{f'\left(x_1\right)}$$

$$f\left(x_2\right)=0.89-\frac{3.13}{5.95}$$

f(x₂) = 0.36

Step 4: Now put n = 2 at x₂ = 0.36

f(x₂) = 3x² + sin(x) = 3(0.36)² + sin(0.36) 

f(x₂) = 0.74

f′(x₂) = 6x+cos(x) = 6(0.36)+cos(0.36)

f′(x₂) =3.09

$$f\left(x_3\right)\:=x_2-\:\frac{f\left(x_2\right)}{f'\left(x_2\right)}$$

$$f\left(x_3\right)=0.36-\frac{0.74}{3.09}$$

f(x₃) = 0.12