To calculate result you have to disable your ad blocker first.
Orthocenter Calculator
To use this calculator, type the three vertices of the triangle, and be careful while typing the x and y coordinates, and click calculate.
Orthocenter calculator
Use the free online orthocenter calculator to solve three vertices of the triangle for its point of concurrency. This tool will provide the steps of the procedure to find the orthocenter.
What is the orthocenter of a triangle?
To put it simply: the point where all three altitudes of a triangle meet is said to be an orthocenter. A triangle has three sides hence three altitudes. It is perpendicular to one side such that it passes the vertex opposite to that side.
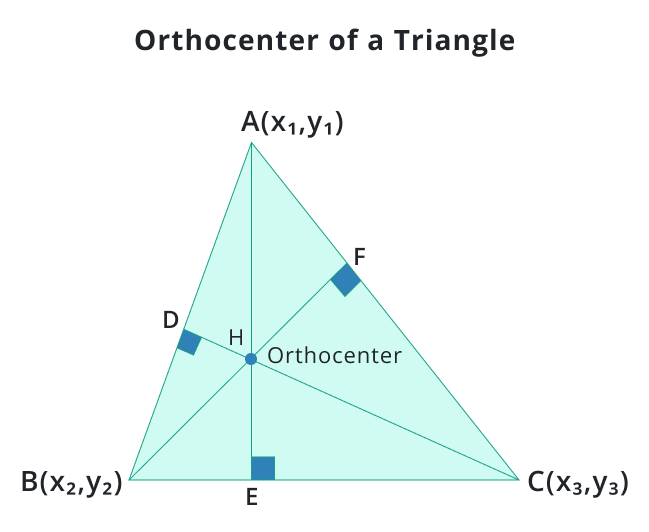
It is called the point of concurrency. For an acute triangle, it is inside the triangle. For an obtuse, it lies outside of the triangle. As for a right-angle triangle, it is on the vertex.
Orthocenter formula:
There are a number of formulas that come into play for this particular calculation. Firstly, you have to find the slope of a line.
For that, you can either use the slope calculator or the formula below.
m = (y2 - y1) / (x2 - x1)
With the help of this value, you can find the slope of the line perpendicular to this side. That will be the slope of altitude.
= -1 / m
Lastly, use this slope and the coordinates of the vertex opposite the side to make an equation. Using two such equations and performing the elimination method, you will get the coordinates of the orthocenter.
How to find the orthocenter?
Use the formulae mentioned above in sequence and solve. Two altitudes are enough to find the orthocenter.
Example:
A triangle has three vertices (2, 3), (3, 4), and (4, 2). Find its orthocenter.
Solution:
Step 1: Draw the triangle for assistance.
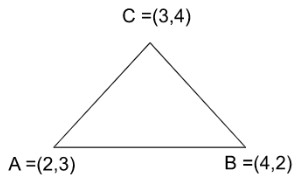
All the lines have a certain slope in the coordinates system. For understanding purposes, the side AB is shown such as it has zero slope.
Step 2: Find the slope of one side.
Choosing side AB.
m = (y2 - y1) / (x2 - x1)
m = (2 - 3) / (4 - 2)
m = -1/2
Step 3: Find the slope of its perpendicular.
= -1/m
= -1/ (-½)
= 2
Step 4: Make the altitude equation.
Using the slope formula.
(y2 - y1) = m (x2 - x1)
(y - 4) = 2(x - 3)
y - 4 = 2x - 6
= 2x - y - 2
Step 5: Find the second equation in a similar fashion.
Choosing side BC.
m = (y2 - y1) / (x2 - x1)
m = (4 - 2) / (3 - 4)
m = 2 /-1 = -2
Find the slope of its perpendicular.
= -1/m
= -1/ (-2/1)
= 1/2
Make the altitude equation. Using the slope formula.
(y2 - y1) = m (x2 - x1)
(y - 3) = 1/2(x - 2)
2y - 6 = x - 2
= x - 2y + 4
Step 6: Use the elimination method.
Arrange the equations
2x - y = 2 … (eq 1)
x - 2y = -4 … (eq 2)
Multiply equation 1 with (-2)
-2(2x - y = 2)
-4x -2y = -4 … (eq 3)
Add equation 2 and equation 3.
x - 2y = -4
-4x -2 y = -4
_________
-3x = -8
x = 2.667
Put this in eq 2.
(2.667) - 2y = -4
-2y = -4 - 2.667
-2y = -6.667
y = 3.333
Hence the orthocenter is as the point (2.667, 3.333)

