To calculate result you have to disable your ad blocker first.
Slope Calculator
To find the slope of a straight line, enter the coordinates of the points in the slope formula calculator.
Table of Contents:
Slope Calculator
This slope finder is an online tool that is used to compute the slope of a line using two points. In the result section of the slope calculator, one can also find slope graphs and slope angles.
What is a Slope?
Slope and gradient are two names for one thing and that is “rise over run”. In simple words, change in the y-axis is divided by change in the x-axis.
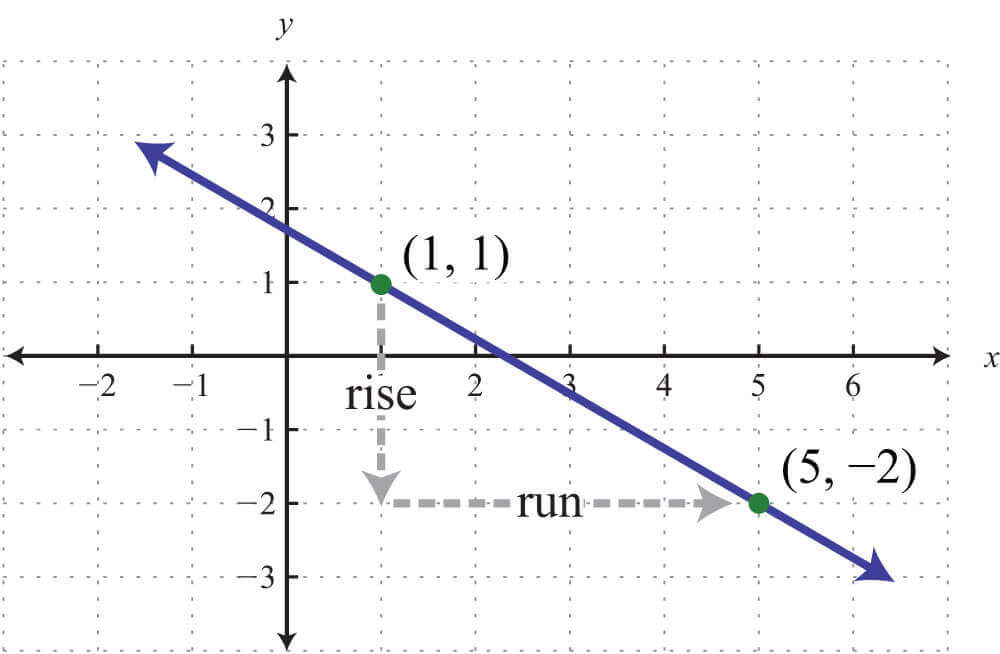
A slope gives information about the line. It tells us if the value of x is increased by “1”, by “how much” the value of y will increase. The slope is usually represented by m.
The slope is also used to make the linear equation using the point slope form or slope intercept form.
Slope Formula
The formula of the slope is:
m = Δy/Δx = y2 - y1 / x2-x1
Where,
yis the position of the point on the y-axis.xis the position of a point on the x-axis.
Types of slope
In mathematics, there are four types of slope and all of these types can be calculated by using this slope calculator.
- Positive Slope
- Negative Slope
- Zero Slope
- Undefined Slope
Positive Slope
In this type of slope, the line of the graph goes upward as x increases. For example, when a person moves upward to the right then the slope of the line is positive. The result of this type of slope is always greater than zero (m > 0).
Negative Slope
In a negative slope, the line of the graph goes downward. For example, when a person moves downward to the right then the slope of the line is negative. The answer of the negative slope is less than zero (m < 0).
Zero Slope
A horizontal line in a graph denotes the zero slope. It is denoted by m=0. The value of the y coordinate (rise) is zero in this type of slope.
Undefined Slope
A vertical line on a graph denotes an undefined slope. In this type of slope, m is undefined. The value of x coordinate (run) is zero in an undefined slope.
How to find a Slope?
Example
A straight line exists in the cartesian plane. The two points of the line are (2,4) and (7,5). Find the slope of a line using these points.
Solution
Step 1: Identify the points.
X1 = 2
X2 = 7
Y1 = 4
Y2 = 5
Step 2: Use the values in the formula.
m = (y2 - y1)/(x2 - x1)
m = (5 - 4)/(7 - 2)
m = 1/5
m = 0.2
Some other examples of slope
| slope of | Result |
| (12, 19) and (18, 7) | Answer m = -2 Step-By-Step Solution Step 1: Write the given values. x1 = 12, x2 = 18, y1 = 19, y2 = 7 Step 2: Take the rise over run formula and evaluate the above values. m = y2 - y1 / x2-x1 m = 7-19/18-12 m = -12/6 m = -2 |
| (-2, -4) and (8, 6) | Answer m = 1 Step-By-Step Solution Step 1: Write the given values. x1 = -2, x2 = 8, y1 = -4, y2 = 6 Step 2: Take the rise over run formula and evaluate the above values. m = y2 - y1 / x2-x1 m = 6-(-4)/8-(-2) m = 10/10 m = 1 |
References
- Khan Academy. (n.d.). What is the Slope? Khan Academy.

