Parabola Calculator

Parabola Calculator

Parabola calculator is used to figure out the parabola in vertex form and standard form using points. It provides both mathematical and graphical solutions to the entered data.

What is a Parabola?

A parabola is a U-shaped curve formed by the set of all points that are equidistant from a fixed point (called the focus) and a fixed straight line (called the directrix). The focus lies on the axis of symmetry, which is a vertical line passing through the vertex of the parabola.

Types of Parabola:

In general, there are two basic forms of the parabola:

1. Standard form
2. Vertex form

Here’s a basic description of these two forms of a parabola:

Standard Form of a Parabola

The standard form of a parabola's equation is given by y = ax² + bx + c, where a, b, and c are constants. The value of a determines the shape of the parabola.

Note: If a is positive, the parabola opens upward; if a is negative, it opens downward.

Vertex Form of a Parabola

The vertex form of a parabola's equation is given by y = a (x - h)² + k, where (h, k) represents the coordinates of the vertex. This form provides insights into the vertex and the direction of the parabola's opening.

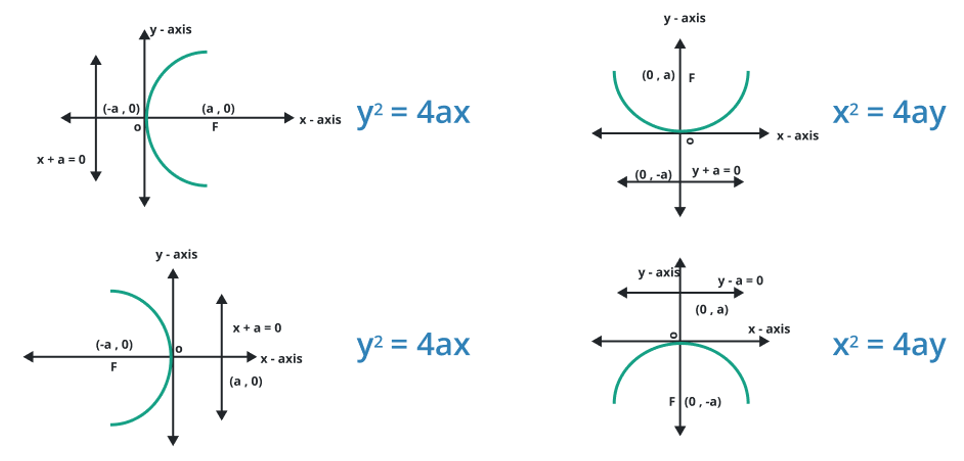
Equation of a Parabola

The general equations of a parabola are:

• y² = – 4ax
• y² = 4ax
• y = a (x – h)² + k
• x² = – 4ay
• x² = 4ay
• x = a (y – k)² +h

The equation of a parabola can be obtained by combining the standard form or the vertex form with additional information about the parabola's vertex, focus, or directrix. By manipulating the equation, we can determine the key characteristics of the parabola.

Properties of a parabola

When we think about the term parabola, our mind redirects to a curved line placed on the cartesian coordinates. There are some properties/components of this term.

• Focus and Directrix
• Axis of Symmetry
• Vertex
• Latus Rectum
• Tangent and Normal

How to graph a parabola?

Graphing a parabola involves plotting its key points, such as the vertex, focus, and directrix, and then sketching the curve accordingly. By using the properties and equations discussed earlier, we can accurately graph different types of parabolas.

Applications of Parabolas

Parabolas have widespread applications in various fields. Here are some notable examples:

Physics:

In physics, parabolic trajectories are commonly observed in projectile motion. The path followed by a thrown object, such as a ball, can be modeled as a parabola under the influence of gravity.

Engineering:    

Parabolic reflectors, such as satellite dishes and car headlights, utilize the reflective properties of parabolas to focus or direct signals and light rays. They play a crucial role in communication systems and optics.

Computer Science:

Parabolic interpolation is a mathematical technique used in computer graphics and numerical methods to estimate values between data points. It helps create smooth curves and surfaces in digital modeling and animation.

How to calculate a parabola?

Example 

Find the vertex form of a parabola having points x = 4, y = 7, h = 3, and k = 9.

Solution:

Step 1: Extract the data

Given points are x = 4, y = 7, h = 3, k = 9

Step 2: Formula:

(x – h)² = 4a(y-k)

Step 3: Solution:

First of all, we have to find a formula for a is following:

a = √ [{h – x₁ * h – x₁} + {k – y₁ * k – y₁}]

a = √ [{(3 – 4) * (3 – 4)} + {(9 – 7) * (9 – 7)}]

a = √ {(-1) * (-1)} + {(2) * (2)}

a = √ (1) + (4)

a = √5

a = 2.236

Now we are putting values in the above formula:

(x – 3)² = 4*2.236(y-9)

(x – 3)² = 8.944(y-9)