To calculate result you have to disable your ad blocker first.
Perpendicular Bisector Calculator
Enter the coordinates of X and Y to construct the perpendicular bisector line equation using perpendicular bisector calculator.
Perpendicular Bisector Calculator
The perpendicular bisector line equation calculator is an online tool that generates an equation for the perpendicular line bisector by using the points on which that line lies. It shows you all steps it used to find the bisector equation.
What is perpendicular bisector?
Perpendicular bisector can be defined as,
“A line which divides a line segment into two equal parts at 90° making a right angle.”
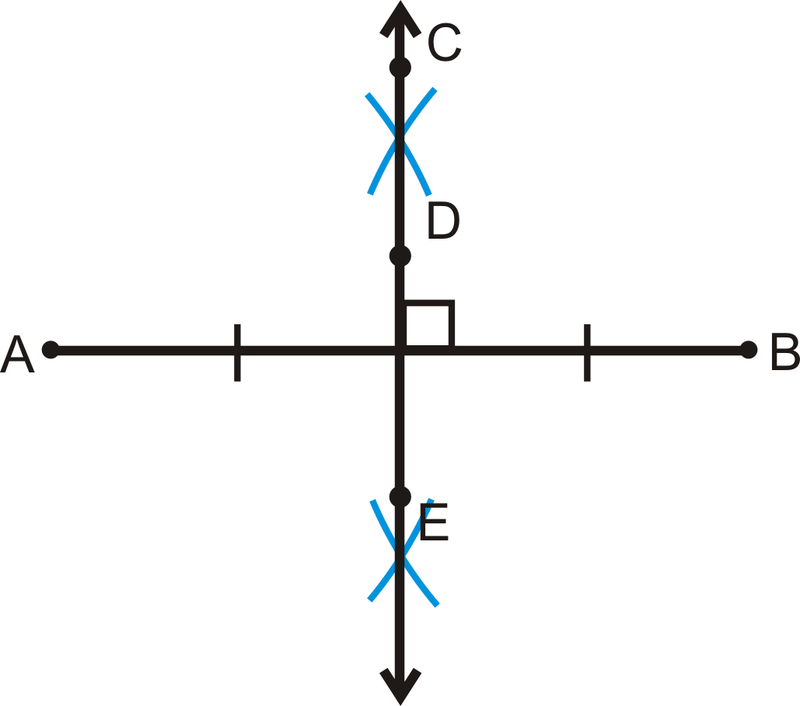
Perpendicular bisector equation
Equation of a perpendicular line bisector is given below.
y – y1 = m ( x – x1)
Where,
- m is slope of the line, and
- x1, y1 are midpoint of the co-ordinates.
How to find equation of perpendicular bisector?
Example:
Find the perpendicular bisector equation of line with the points (6, 7), (4, 3).
Solution:
Step 1: identify the values.
x1 = 6, x2 = 4
y1 = 7, y2 = 3
Step 2: Find the midpoint using the given points.
Midpoint = (x1 + x2)/2, ( y1 + y2 )/2
= (6+4)/2, (7 +3)/2
= (10/2, 10/2)
= (5, 5)
Midpoint coordinates (x1 , y2) = (5, 5)
Step 3: Find the slope of line:
Slope m = (y 2 - y1)/(x 2 - x1)
(3-7)/(4-6)
= 2
Step 4: Take the negative reciprocal of slope.
m = - (1/2) = - 0.5
Step 5: Place the values in perpendicular bisector equation.
y – y1 = m(x – x1)
y – 5 = -0.5(x – 5)
y = -0.5x + 7.5

