Dependent Events: Definition, Types, Applications, and Examples

Publish Date: 18 Nov, 2023

Table of Content

01. Dependent Events
02. Types of Dependent Events
03. The Impact of Dependent Events
04. Strategies for Analyzing Dependent Events:
05. Real-Life Applications of Dependent Events:
06. How to calculate dependent events?

Dependent events are critical in probability theory for understanding the links between different outcomes. The interdependence of these circumstances is defined by the notion that the outgrowth of one event influences the possibility or circumstance of another.

In this post, we will explore dependent events, including its definition, types, and uses in daily life.

Dependent Events

A dependent event is defined by the interdependence of events, in which the circumstance non-occurrence of another determines the result or possibility of one event.

The actuality or absence of the first event directly influences the probability or circumstance of the alternate event. Because the probabilities must be assessed in relation to one another, this dependency adds an interconnectedness component.

Formula:

P (Event A and Event B) = P (Event A) * P (Event B | Event A)

Types of Dependent Events

The types of dependent events are as follows:

Conditional Probability
Sequential Events
Complementary Events

Conditional Probability:

Conditional probability is a fundamental aspect of dependent events. It involves calculating the probability of an event given that another event has formerly passed. The probability of the alternate event is told by the knowledge or circumstance of the first event.

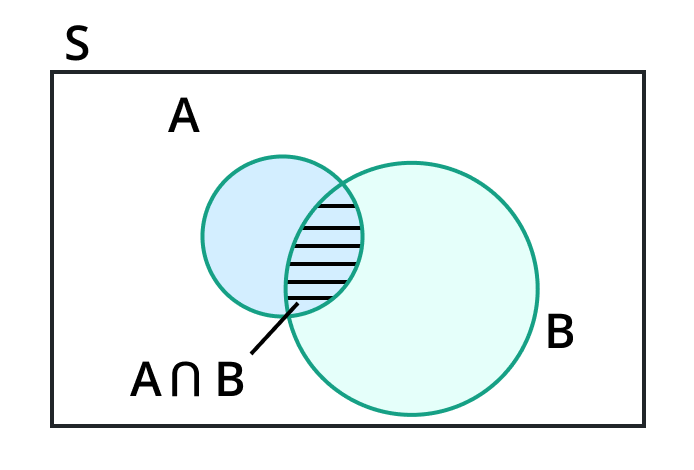
conditional probability

Conditional probability is often expressed as P(A|B), where A and B are events, and “|” represents “given.”

P(A|B) = N(A∩B) / N(B)

P(B|A) = N(A∩B) / N(A)

Sequential Events:

Sequential events are a common type of dependent event. They occur in a specific order, and the result of each event affects the probability of posterior events.

For example, drawing cards from a deck without replacement is a sequential event. The probability of drawing a certain card changes based on the cards already drawn.

Complementary Events:

Complementary events are dependent events where the outcomes are mutually exclusive and exhaustive. The incident or reality of one event affects the probability of the other event.

complementary events

For example:

In a coin toss, “heads” and “tails” are complementary. If the first toss results in heads, the probability of tails in the subsequent toss changes.

The Impact of Dependent Events

Dependent events have powerful meaning in numerous areas, including risk assessment, decision-making, and resource allocation.

Risk Assessment:

In risk assessment, understanding the dependency between events is crucial. By evaluating how one event impacts the probability of another, experts can estimate the potential risks involved and develop appropriate strategies to reduce the risk.

Decision Making:

Dependent events influence decision-making processes. For example, in project management, the completion of one task might be essential for starting another. Identifying dependent events helps in planning and scheduling activities effectively.

Resource Allocation:

Dependent events also affect resource allocation. Organizations need to consider the dependencies between different tasks and allocate resources accordingly. Failing to account for these dependencies can lead to delays or inefficiencies in project execution.

Strategies for Analyzing Dependent Events:

To analyze dependent events effectively, several strategies and tools can be employed.

Tree Diagrams:

Tree diagrams visually represent dependent events, showcasing different possible outcomes and their associated probabilities. They help in organizing and understanding complex sequences of events.

Venn Diagrams:

Venn diagrams are useful for illustrating the relationships between events. They characterize overlapping areas to showcase commonalities and dependencies between different sets of events.

Probability Formulas:

Probability formulas, such as the multiplication and addition rules, provide a mathematical framework for calculating the probabilities of dependent events. These formulas consider the relationships and dependencies between events.

Real-Life Applications of Dependent Events:

Some real-life applications of dependent events are as follows:

Weather Forecasting
Stock Market Analysis
Medical Diagnostics

Weather Forecasting:

Weather forecasting heavily relies on dependent events. Meteorologists analyze various atmospheric conditions to predict the weather accurately. Temperature, humidity, wind speed, and cloud cover are such factors that are all mutually dependent and changes in one can impact the probability of specific weather patterns.

Stock Market Analysis:

In finance, stock market analysis involves assessing the interdependence of different events. Stock prices are influenced by numerous factors, including company performance, economic indicators, and global events. Understanding the dependency between these variables helps investors make informed decisions.

Medical Diagnostics:

Medical diagnostics also involve dependent events Doctors use a combination of symptoms, medical history, and test results to determine the possibility of a disease. The incident or reality of a particular disorder may significantly change the possibility of a unique diagnosis.