Probability Calculator

Probability Calculator

Probability calculator is a free online tool that quickly calculates probability in three different possibilities: single, dependent, and independent. This probability solver finds the possibility of one or more occurrences and success in a single event selection and provides value in decimals or percentages.

Moreover, it allows multiple selections in dependent or independent events to find probability of “A” and “B” using a suitable formula for each case. This conditional probability calculator also provides detailed steps that help to understand the process of probability calculation.

What is Probability?

In statistics, probability is a measure used to quantify the likelihood of the occurrence of any event. The value of probability always lies between 0 and 1 or as percentages from 0% to 100%.

If the probability value is 1 or 100%, it means the event will certainly occur, while a value of 0 or 0% means there is no chance of the event happening. Sometimes, the likelihood of an event occurring depends on many factors, such as whether the events are dependent, independent, or conditionally of one event to another.

Based on these factors, probability can be categorized into many other types, such as classical, empirical, Axiomatic, marginal, joint, and conditional probability.

Probability Formulas

There are many probability formulas due to the many types of probability and the occurrence of events, dependently or independently. These are all used to calculate the likelihood value for its occurrence type or nature of the event, such as single, dependent, and independent events.

Some well-known are explained below:

1.    Formulas for Single Event

Single-event formulas are used to find the likelihood or probability of one event that occurs in a single trial.

Formula for Probability of Event (A)

The probability for event “A” is written as P(A). The formula used to find the probability is:

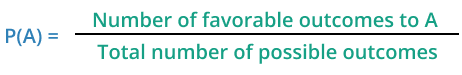
Simply written as: P(A) = n(A) / n(S), and its percentage can be found by P(A)% = P(A) x 100.

Formula for Complement of Event

The complement of probability tells the chances of it NOT occurring. It has a simple formula that stated as:

P(A^c) = 1 - P(A),  and  P(A^c)% = [1 – P(A)] x 100.

1.    Formulas for Independent Events

These formulas are used to find the probability of two independent events that occur without affecting the possibility of other events. Formulas are given below:

Multiplication Rule of Probability

It is used to calculate the probability of A and B occurring together independently, represented by P(A∩B):

P(A∩B) = P(A) × P(B)

It is modified as if the values of two are given and one is missing:

P(A) = P(A∩B)/P(B) or P(B) = P(A∩B)/P(A)

Addition Rule of Probability

This rule is used to calculate probability of A and B by including the probabilities of each event individually, that mathematically shown as P(A∪B):

P(A∪B) = P(A) + P(B) - P(A∩B)

Finding One Probability if others are given

This formula is used to find the probability of event P(A) while “P(B)” & “P(A∪B)”  values are given.

P(A) = (P(A∪B) - P(B)) / (1 - P(B))

2.    Formulas for Dependent Events

The formulas below are used to calculate probability of a dependent event in which the outcome of one event affects to occurrence of another event.

Conditional Probability Rule

It calculates conditional probabilities such as P(A|B), P(B|A), or others, if one is missing from all. 

P(A|B) = P(A∩B) / P(B) or P(B|A) = P(A∩B) / P(A)

Multiplication Rule for Dependent

It is used to find probability of both events occurring together dependently that mathematically stated as P(A∩B):

P(A∩B) = P(B) × P(A|B)

Baye’s Theorem or Baye’s Rule

It is used to calculate the likelihood value of event A given under B that has already occurred by using the reverse conditional probability and can be represented as:   

P(A|B) = P(B|A) × P(A) / P(B)

How to calculate Probability?

For a quick solution, you use our above probability calculator. However, if you want to understand how to find probability manually and improve your concept to perform any experiment. Then see the example below in which we solve different problems for single, dependent, and independent events. 

Probability Examples

Here we solved a probability example with detailed steps that help to understand how to calculate probability of any event.

Example 1: (For single Event)

What is the probability to choosing 7 cards if you draw one card from a deck of playing cards?

Solution:

Step 1: First, note the data that we need.

As we know, 52 cards in a deck means total outcomes are 52. And as each deck contains one card of 7, it means 7 events happen 4 times. Hence,

n(E) = 4

n(T) = 52

Step 2: Now, put value in the single event formula.

P(7) = 4/52

P(7) = 0.077 

Hence, this is the answer. Use the percentage calculator to convert it into a percentage.

Example 2: (For Independent Event)

Calculate probability of both events if getting heads to toss a coin and 4 to rolling a standard die.

Step 1:Note event and possible outcome from probability problem.

Event A: Head on coin,

On the toss there are a two possible outcomes (Heads, Tails).
n (A) = 1, n(S) = 2

Event B: Favorable 4 on the die.

To die roll there are a 6 possible outcomes.
n (B) = 1, n(S) = 6

Step 2: Calculate the probability individual event with single event formula.

P(A) = 1/2 = 0.5

P(B)=1/6 = 0.1667

Step 3: Now, find the joint probability of both A and B by putting above values in multiplication rule.

P(A∩B) = P(A) × P(B)

  = 0.5 × 0.1667 = 0.0833

Example 3: (For Dependent Event)

What is the probability of king’s card if draw Two Cards without replacement, both are king?

Step 1: Note the event and possible outcome for each.

Event “A” = First card drawn is king.

n(A) = 4, n(S) = 52

Event “B|A” = Second card drawn is also King after the first taken from deck.

                              n(B) = 3, n(S) = 51

Step 2: Now, calculate probability of first and second event, individually.

P(A) = 4/52 =1/13 = 0.0769

P(B∣A) = 3/51 = 0.0588

Step 3: Finally, calculate probability of both event together by putting above values in both joint probability formula.

P(A∩B)= P(A)×P(B∣A)

                                = 0.0769 × 0.0588 = 0.0045

Thus, probability of both events is 0.0045. To verify the results of all above example use our above probability calculator.