Reynolds Number Calculator

Reynolds number calculator  

Know the type of fluid flow using the Reynolds number calculator. It can change its interface to find any unknown quantity of the formula. 

What is Reynold's number? 

Reynold’s number is a quantity that identifies the nature of the flow. The concept is named after Osborne Reynolds, a prominent British engineer and physicist.

It is a ratio between two forces which is why it is dimensionless. It basically characterizes the fluid flow as either turbulent or laminar.

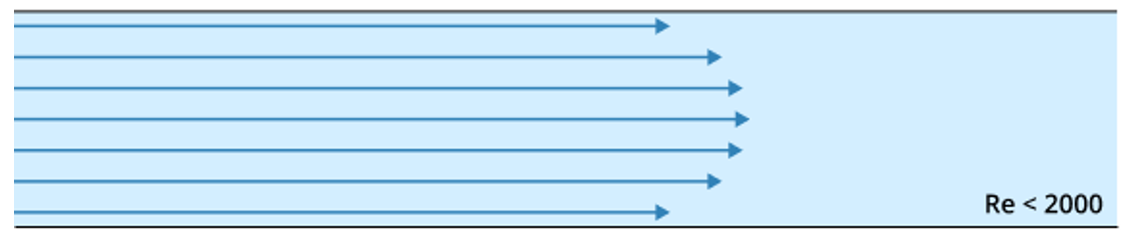
Laminar Flow:

This is a smooth and orderly fluid motion, where particles of the fluid flow in parallel lines. This type of flow is typically found at lower velocities and smaller scales.

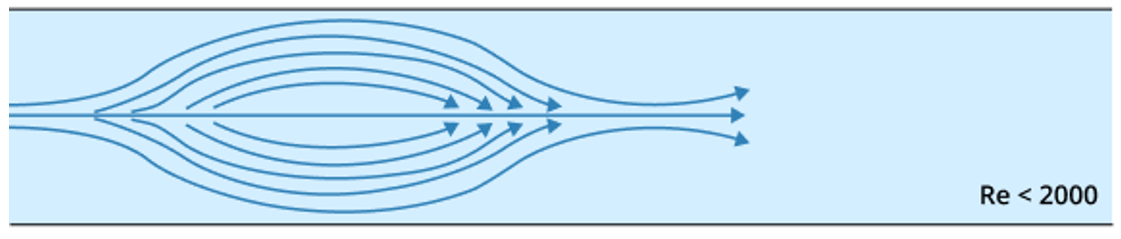
Turbulent Flow:

This is characterized by chaotic and disordered fluid motion. Here, the fluid particles move randomly and create swirls or eddies. This type of flow is often found at higher velocities and larger scales.

Reynold’s Number Formula

It is calculated by finding the ratio between inertial forces and viscous forces. The formula used is:

Re = ρuL/μ

where:

• Re is the Reynolds number,
• ρ is the fluid density,
• u is the fluid velocity,
• L is a characteristic length scale (for example, the diameter of a pipe if the fluid is flowing through a pipe), and
• μ is the dynamic viscosity of the fluid.

Alternatively, it can be expressed in terms of the kinematic viscosity (ν, which is μ/ρ) as:

Re = uL/ν

How to find Reynold’s number?

Use the above Reynold’s number calculator to quickly find its value. Alternatively, put all of the required values in the formula and solve manually. Let's solve an example to understand better.

Consider water flowing through a pipe. The diameter (D) of the pipe is 0.1 m, the velocity (u) of the water is 1 m/s, and the density (ρ) of the water is approximately 1000 kg/m³. 

The dynamic viscosity (μ) of water at room temperature is approximately 1.00 x 10^-3 Pa.s (Pascal-seconds).

The Reynolds number is given by the formula:

Re = ρuD/μ

Substitute the given values into the formula:

Re = (1000 kg/m³ * 1 m/s * 0.1 m) / (1.00 x 10^-3 Pa.s)

Re = 100,000

A Reynolds number of 100,000 suggests that the flow is likely to be turbulent, as it is significantly greater than the commonly used threshold of 2300 for transition to turbulence in pipe flow.

Applications of Reynolds Number

Understanding the Reynolds number has numerous practical applications:

Designing Vehicles:

Engineers use the Reynolds number when designing cars, airplanes, or submarines. They aim to minimize turbulent flow, reducing drag and increasing efficiency.

Environmental Studies:

Researchers studying river currents or wind patterns use the Reynolds number to predict flow patterns.

Medical Applications:

In medical science, the concept is applied to understand blood flow in the human body, which aids in designing medical devices like heart pumps.

Industrial Applications:

In industries, it's used to design pipelines for fluid transport, enabling the prediction of pressure drops and optimizing energy use.