To calculate result you have to disable your ad blocker first.
Tangent calculator
To solve the tangent trigonometric function, enter the value of tan(x) in the input box, select the degree or radian from the list and hit calculate button using this tangent calculator.
The tangent calculator is designed to provide the values of trigonometric function tan. You can calculate the value of tan for both radians and degrees by the tangent finder.
How to use the tangent solver?
To use the tan calculator, you will have to
- Enter the value of the angle.
- Choose the angle unit i.e degrees or radians
- Lastly, click calculate.
What is tangent?
Tangent aka tan is the ratio of perpendicular to the base for a right-angle triangle. It is also defined as the opposite over adjacent for a normal triangle.
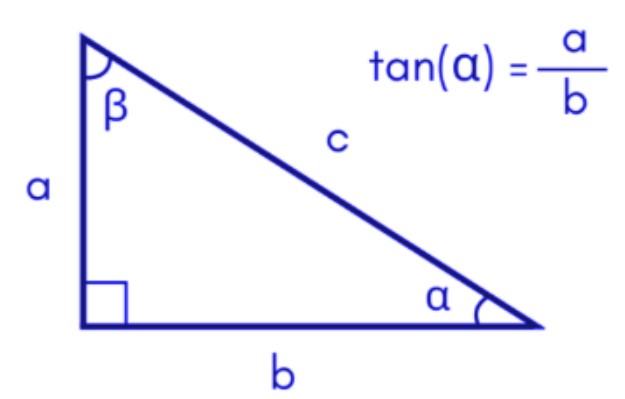
It is one of the three main ratios of trigonometry, others are sine and cos.
Tangent has its uses in almost every field.
If you want to find something similar to hypotenuse or slope, tan is the function you will need. For kinematics in robotics, measurements in construction, flight path in the air traffic, and many more.
How to find tangents?
The formula to find tan lies in its own definition i.e
tan(x) = base/hypotenuse = opposite / adjacent
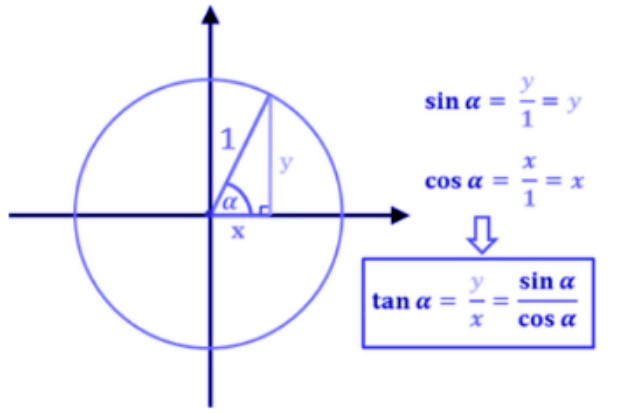
It is also possible to compute tan using the other two basic trig ratios i.e sine and cosine.
Tan (x) = sinx / cosx
Example:
Find the value of tan(x) if sine x is ½ and cosine x is -√3/2.
Solution:
Step 1: Write the given values.
Sin x = ½
Cos x = -√3/2
Step 2: Use the formula.
Tanx = sinx /cosx
Tanx = (½) / -√3/2
= 0.5 / - 0.866
= - 0.58
Since it's a ratio, there is no unit.
Tangent chart:
The tan chart contains the values of this trig function for common angles like 30o, 90o, and 180o.
| Angle (Radians) | Angle (degrees) | Tangent |
| 0 | 0o | 0 |
| π / 6 | 30 | 1/√3 |
| π / 4 | 45 | 1 |
| π / 3 | 60 | √3 |
| π / 2 | 90 | undefined |
| 2π / 3 | 120 | -√3 |
| π | 180 | 0 |
| 7π/ 6 | 210 | 1/√3 |
| 3π / 2 | 270 | undefined |
| 5π / 3 | 300 | -√3 |
| 11π / 6 | 330 | -1/√3 |
| 2π | 360 | 0 |
Inverse of tan:
The inverse of tan (tan^-1) is called arctan. It is used to find the angle through a tan value. For example, if tan (60) is √3 then arctan of √3 is 60 degrees.

