To calculate result you have to disable your ad blocker first.
Vertex Form Calculator
Choose the equation form and enter the required values in the vertex form calculator to find the vertex of a parabola.
Vertex Form Calculator
Vertex form calculator is an online tool that helps to find the vertex point of a quadratic equation graph. You can find vertices using both standard or vertex forms.
The vertex form converter will calculate the y-intercept as well. You can also convert the standard form to vertex form through this calculator.
What is the vertex form?
The vertex form is one of the two main ways to represent a quadratic equation. The syntax of the equation involves the vertex, the maximum or minimum point of the parabola, hence the name is vertex form.
It includes three variables a, h, and k as shown.
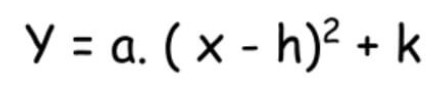
The letter a represents concave up and down. The letter h represents the x coordinate and the letter k represents the y coordinate.
Solve for the values of x using the quadratic equation calculator.
How to convert standard form to vertex form?
Two main things that we need to do while this conversion is separating the x2 and completing the square. Let’s take the equation 2x2 - 8x + 2.
To separate the x2, we will have to divide the whole equation by 2.
= (2x2 - 8x + 2) / 2
= x2 - 4x + 1
Complete the square by adding and subtracting the suitable value. Divide the 4x by 2 and take its square.
= (4/2)2 = 22 = 4
Use the calculated value to complete the square.
= x2 - 4x + 4 - 4 + 1
= 1(x - 2)2 - 3
How to find the vertex?
You can find the vertex from both standard and vertex forms manually. But the fastest mean will be the vertex form converter. To learn how to calculate the vertex, keep reading.
Through standard form:
The standard form of a quadratic equation is ax2 + bx + c. There are two formulas that are used to find the x and y coordinates. These formulas are:
h = -b / (2a)
k = c - b2 / (4a)
Example:
Find the vertex of the equation 8x2 - 7x + 1.
Solution:
Step 1: Identify the values.
a = 8
b = -7
c = 1
Step 2: Put the values in the formulas.
h = -b / (2a)
h = -(-7) / 2(8)
h = 7/16
h = 0.44
k = c - b2 / (4a)
k = 1 - (-7)2 / 4(8)
k = 1 - 49 / 32
k = 1 - 1.53
k = 0.53
Through vertex form:
It is rather easy to find the vertex using the vertex form equation as all you have to do is identify the value of h and k.
Example:
Find the vertex from the following parabolic equation.
y = 6( x - 1)2 + 7
Solution:
Compare the equation with the general vertex form and identify the value of h and k.
h = 1
k = 7

