To calculate result you have to disable your ad blocker first.
Wronskian Calculator
To use wronskian calculator, enter the comma-separated value of a function, press the enter key, or hit the calculate button for the solution.
Wronskian Calculator
Wronskian calculator calculates the wronskian value of a set of functions to evaluate whether the function is linearly independent or not. This generates a scalar value and also provides steps.
What is meant by wronskian?
It is a mathematical technique that is used to determine whether the given set of functions is linearly dependent or independent. The wronskian is a determinant whose entries are the function and their corresponding derivatives.
If the value of wornksian is zero at some interval, then the functions are linearly dependent otherwise the functions are linearly dependent.
Formula:
If we have functions f1, f2, f3… fn. then the determinate of n by n matrix with the n-1 derivative of these functions.
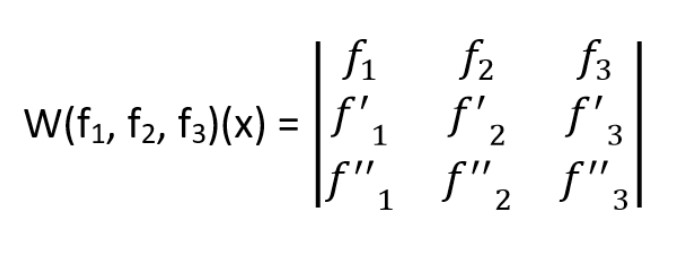
How to calculate wronskian problems?
In this section, we have solved a mathematical example by briefly describing each side of the problem with steps.
Example
By using the wronskian method find the value of the functional value is cos(x), sin(x), cos(2x).
Solution:
Step 1: First we have selected the functions which are three-dimensional.
f1= cos(x), f2= sin(x), f3= cos(2x)
Step 2: The wronskian is given by
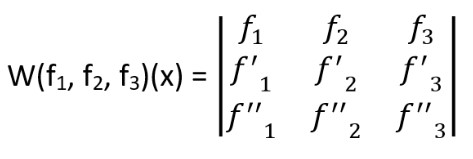
Step 3: Now we have to find the derivative of the function
f1= cos(x), f’1= -sin(x), f’’1= -cos(x)
f2=sin(x), f’2= cos(x), f’’2= -sin(x)
f3= cos(x), f’3= -2sin(2x), f’’3=-4cos(2x)
Step 4: Put the values in the corresponding positions
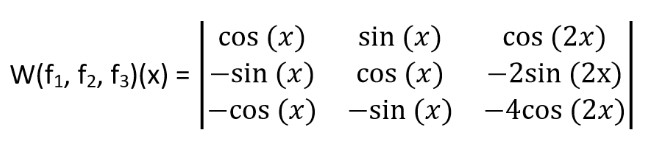
Step 5: Now simplify the determinant of order 3 by 3.
W(f1, f2, f3)(x) = -3cos(2x)

