Improper Fraction: Definition, Conversion, and Examples

A fraction is a method of expressing a part of the whole. It has two numbers separated by a line: the top number is the numerator, and the bottom number is the denominator. Such as the fraction 4/7, where 2 is the numerator, and 5 is the denominator.

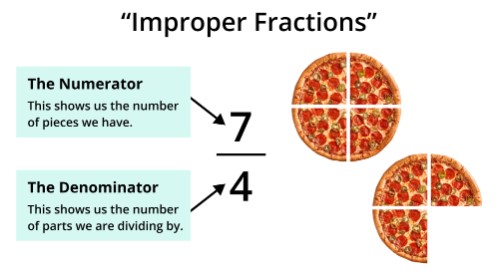
When the numerator of a fraction is greater than or equal to the denominator, we call it an improper fraction. For instance, 7/4 is an improper fraction, because the numerator (7) is greater than the denominator (4).

In this article, we will explore the concept of improper fractions, including its definition, conversion to mixed numbers, conversion from mixed numbers, properties, and applications.

What is an Improper Fraction?

An improper fraction is a type of fraction in which the numerator (number on the top) is greater than or equal to the denominator (number on the bottom).

Mathematically, the improper fraction is written in the form of p/q, where p ≥ q.

Following are some examples of improper fractions:

• 7/4
• 11/8
• 19/17
• 5/3

Method for Simplifying Improper Fractions

In some cases, it may be necessary to simplify an improper fraction to its lowest terms. To do this, we find the Highest Common Factor (HCF) of the numerator and denominator and divide both by it. This process is sometimes referred to as reducing the fraction. Let's show this with an example.

Example:

Simplify 24/36.

The HCF of 24 and 36 is 12. Divide both the numerator and denominator by 12:

24 ÷ 12 = 2

36 ÷ 12 = 3

Thus, 24/36 can be reduced to its simplest form of 2/3.

Conversion of an Improper Fraction to a Mixed Number

Converting an improper fraction to a mixed number can be helpful in certain situations. A mixed number is a representation that combines a whole number and a proper fraction into a single expression.  The process of converting an improper fraction to a mixed number involves dividing the numerator by the denominator. The quotient obtained from this division represents the whole number part, while the remainder becomes the numerator of the proper fraction.

Example:

Convert 9/4 to a mixed number.

9 ÷ 4 = 2 remainder 1

Therefore, 9/4 can be expressed as the mixed number 2 ¼

How to Write the Mixed Number in an Improper Fraction?

We can convert a mixed number to an improper fraction by following a simple process. First, we multiply the whole number part by the denominator and then add the numerator to the result. The outcome of this calculation becomes the new numerator, while the denominator remains unchanged.

Example:

Write down the mixed number 3 2/5 into improper fractions.

3 × 5 + 2 = 15 + 2 = 17

Therefore, 3 2/5 can be expressed as the improper fraction 17/5.

Mathematical Operations On Improper Fractions

Performing operations with improper fractions follows the same principles as operations with other fractions. Let's explore the basic operations of addition, subtraction, multiplication, and division with improper fractions.

Addition and subtraction of Improper fraction

We make sure the denominators are the same before adding or subtracting improper fractions. Once the denominators are equal, we can add or subtract the numerators and retain the denominator. Let's look at its example.

Example:

Add 5/6 and 7/6.

We can add the numerators since the denominators are identical:

5/6 + 7/6 = (5 + 7)/6 = 12/6 = 2

Improper fraction multiplication

While multiplying improper fractions, we simply multiply the numerators and denominators. The resulting product is another improper fraction. Let's consider an example.

Example:

Multiply 3/4 by 5/6.

(3/4) × (5/6) = (3 × 5) / (4 × 6)

                   = 15 / 24

Dividing Improper Fractions

To divide improper fractions, multiply the 1^st fraction by the multiplicative inverse of the 2^nd fraction. The multiplicative inverse is obtained by flipping the numerator and the denominator.

Example:

Divide 7/8 by 2/3.

(7/8) ÷ (2/3) = (7/8) × (3/2)

                       = (7 × 3) / (8 × 2)

                       = 21/16

Applications of Improper Fractions

Improper fractions have several practical applications in the real world. Some of these are here:

Engineering and Architecture

Improper fractions are commonly used in engineering and architecture to represent precise measurements and dimensions. For instance, when designing a structure, a beam's length may be expressed as 15 3/8 feet or a bolt's diameter as 7/16 inches.

Cooking and Recipes

When baking a cake, you might need to use an improper fraction to represent the amount of flour you need. For example; if the recipe calls for 2 ½ cups of flour, you would use the improper fraction 5/2 to represent this amount.

Drug Dosages

In the medical field, improper fractions are used to represent drug dosages. Medications may be prescribed in quantities like 2 ¾ tablets or 1 ½ teaspoons, ensuring accurate administration.

Sewing and Fabrics

Improper fractions find application in sewing and fabric measurements. They can represent lengths, such as    4 ½ yards of fabric needed for a project, enabling accurate cutting and stitching.

Solved Examples of Improper Fractions

Example 1:

Convert 17/4 into a mixed number.

Solution:

Step 01: Divide the numerator by the denominator.

Divide 17 by 4: 17 ÷ 4 = 4 with a remainder of 1.

Step 02: The quotient becomes the whole number, and the remainder becomes the numerator of the fractional part.

Therefore, the mixed number of 17/4 is 4 ¼. 

Example 2:

Add 7/3 and 5/2.

Solution:

Step 1: Evaluate the common denominator.

In this case, 6 is the LCM of 3 and 2. Therefore, we will use 6 as the common denominator.

Step 2:  Convert the fractions so that they share the same denominator.

To convert 7/3, multiply both the denominator and numerator by 2, resulting in 14/6.

To convert 5/2, multiply both the denominator and numerator by 3, resulting in 15/6.

Step 3: Add the fractions.

Since both fractions now have the same denominator, we can add them.

14/6 + 15/6 = (14 + 15) / 6 = 29/6.

Thus, the sum of 7/3 and 5/2 is 29/6.

Conclusion

In this article, we have discussed the definition of improper fractions in detail. We learned how to simply the improper fraction, converting it into mixed form, and mixed form into proper fraction. We explored the mathematical operations with improper fractions. We described its importance in our lives. At last, we did examples for our readers to understand it in a better manner.