Bisection Method Calculator

Bisection Method Calculator

The bisection method calculator is a simple and easy to use online calculator that helps to find the root of a function and shows all the relevant steps. 
This calculator takes the values of the lower and upper bounds of the function with the tolerance and desired number of iterations to compute the root of the function with its graphical representation.

What is Bisection Method?

The bisection method is an important numerical method that is used in determining the root of a continuous and a real valued function within a specific interval. It is an iterative approach that uses the intermediate value theorem (IVT) which states that a continuity of the function changing sign over an interval must have at least one root within that interval.

Procedure to Apply the Bisection Method

1. Initialization

• Select an interval ([a, b]) where the function changes sign.
• Check (f (a) * f (b) < 0) to ensure the existence of a root in the interval.

2. Iteration

• Divide the interval in half and evaluate the function at the midpoint (c = (a + b) / 2).
• Determine the subinterval containing the root based on the sign of (f(c)).
• Update the interval to be the subinterval containing the root.

3. Convergence

• Repeat the process until an adequate accurate root is found commonly when the function value is close to zero or the interval becomes small enough.

4. Out Put

• The final interval or midpoint provides an approximation of the root.

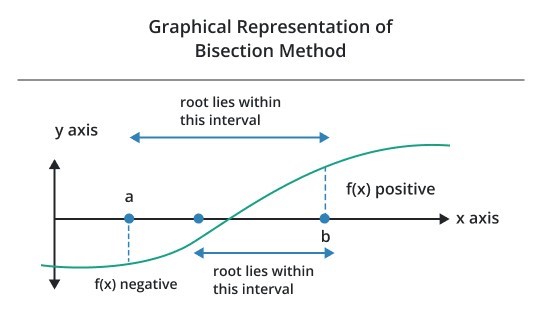
Graphical Representation of Bisection Method

The graphical representation of bisection method shows roots lie between the interval values [a, b] by determining the value of the function. If the product of the functional values f(a) and f(b) is negative or less than zero then roots lie between the interval values. Its representation is shown below.

Limitations of Bisection Method

1. Convergence Rate

• Linear convergence doubles the number of correct digits with each iteration.

2. Initial Interval Requirement

• Relies on an initial interval where the function changes sign.

3. Single Root

• Suitable for finding a single root within the given interval.

4. No Derivative Information

• Does not use derivative information possibly slowing down convergence.

5. No Suitable for Complex Root

• Less useful for those functions if roots are complex numbers.

Regardless of these limitations, the bisection method is a good choice for finding roots, especially for functions that are not smooth or differentiable everywhere.

How to apply Bisection Method?

Find the root of the equation 2x⁵ + 3x + 1 = 0 for x ∈ [-1, 1] with the tolerance 0.01 using bisection method.

Solution

Step 1: Write the given information from question.

      2x⁵ + 3x + 1 = 0 and x ∈ [-1, 1]

     Tolerance = 0.01

Step 2: To ensure the existence of the root in the given interval, we will compute the value of the function at endpoints.

f (a) = f (-1) = 2 (-1)⁵ + 3 (-1) + 1 = -4

f (b) = f (1) = 2 (1)⁵ + 3 (1) + 1 = 6

As the given function changes its sign at the endpoints of the interval it ensures the existence of the root in the given interval.

Step 3: Consider "c" as the midpoint of the interval. Now we will perform iterations to determine the approximate root.

Iteration 1

a = -1.0,   b = 0.0,   c = 0.0

f (c) = 1.0

Iteration 2

a = -0.5,  b = 0.0,  c = -0.5

f (c) = -0.5625

Iteration 3

a = -0.5,  b = -0.25,  c = -0.25

f (c) = 0.248046875

Iteration 4

a = -0.375,  b = -0.25,  c = -0.375

f (c) = -0.13983154296875

Iteration 5

a = -0.375,  b = -0.3125,  c = -0.3125

f (c) = 0.05653953552246094

Iteration 6

a = -0.34375,  b = -0.3125,  c = -0.34375

f (c) = -0.040849387645721436

Now we can observe that:

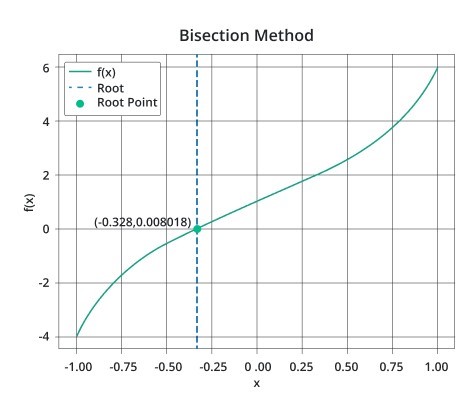
c = (-0.34375 + (-0.3125)) / 2 = -0.328125

Now, put the values of "c" in given function.

f (c) = f (-0.328125) = 2 (-0.328125)⁵ + 3 (-0.328125) + 1 = 0.008018 < tolerance

So, the solution of the equation 2x⁵ + 3x + 1 = 0 is - 0.328125 with a tolerance of 0.01. 
We can observe it graphically as in the following.