Continuity Calculator

Continuity Calculator

Continuity calculator finds whether the function is continuous or discontinuous. This continuous calculator finds the result with steps in a couple of seconds. 

What is continuity?

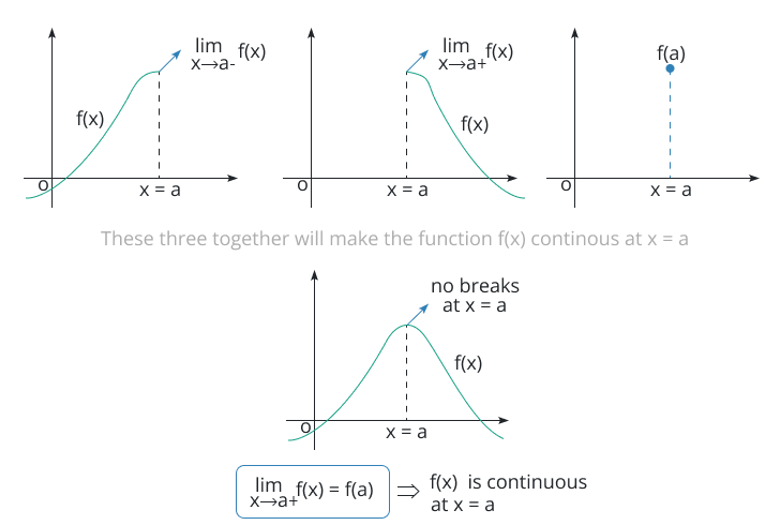
In calculus, continuity is a term used to check whether the function is continuous or not on the given interval. The continuity can be defined as if the graph of a function does not have any hole or breakage. If there is a hole or break in the graph then it should be discontinuous. 

The concept of continuity is very essential in calculus as the differential is only applicable when the function is continuous at a point. If the function is not continuous then differentiation is not possible. 

Mathematically, a function must be continuous at a point x = a if it satisfies the following conditions. 

1. f(a) exists (function must be defined on “a”) 
2. lim_x→a f(x) exists (limit of the function at “a” must exist)
3. f(a) = limx→a f(x) 

If all three conditions are satisfied then the function is continuous otherwise it is discontinuous. 

How to calculate the continuity?

Here is a solved example of continuity to learn how to calculate it manually. 

Example 1

Check whether a given function is continuous or not at x = 2.

f(x) = 3x2 + 4x + 5

Solution 

Step 1: Check whether the function is defined or not at x = 2.

f(2) = 3(2)2 + 4(2) + 5

      = 3(4) + 4(2) + 5

      = 12 + 8 + 5

      = 25

Hence, the function is defined at x = 2.

Step 2: Evaluate the limit of the given function.

limx→2 [3x2 + 4x + 5] = limx→2 [3x2] + limx→2 [4x] + limx→2 [5]

                                  = 3lim_x→2 [x²] + 4lim_x→2 [x] + lim_x→2 [5]

                                  = 3[22] + 4[2] + [5]

                                  = 3(4) + 4(2) + 5

                                  = 12 + 8 + 5

                                  = 25

Hence, the limit of the function exists.

Step 3: Check the third condition of continuity.

f(2) = limx→2 f(x) 

25 = 25

Hence the function is continuous as all the conditions are satisfied. 

Example 2:

Check whether a given function is continuous or not at x = 0.

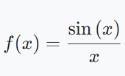
Solution 

Step 1: Check whether the function is defined or not at x = 0.

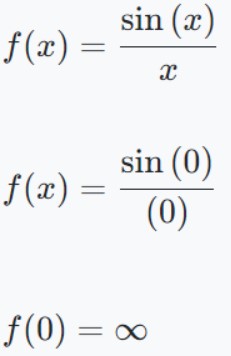
Hence, the function is not defined at x = 0.

Step 2: Calculate the limit of the given function.

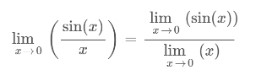
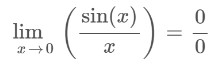
As the function gives 0/0 form, apply L’hopital’s rule of limit to evaluate the result. 

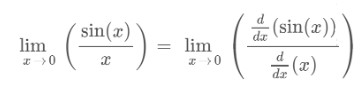
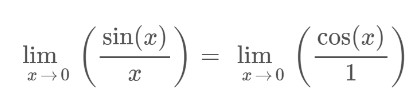
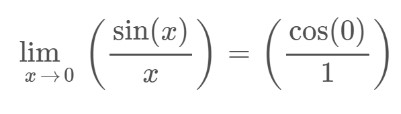
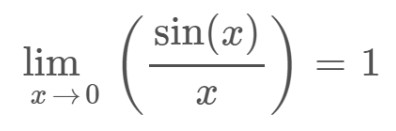
Step 3: Check the third condition of continuity.

f(0) = limx→0 f(x) 

∞ = 1

Condition 1 & 3 is not satisfied. So, the function is discontinuous.